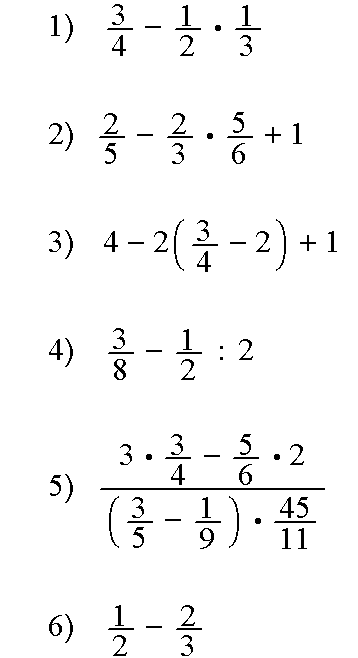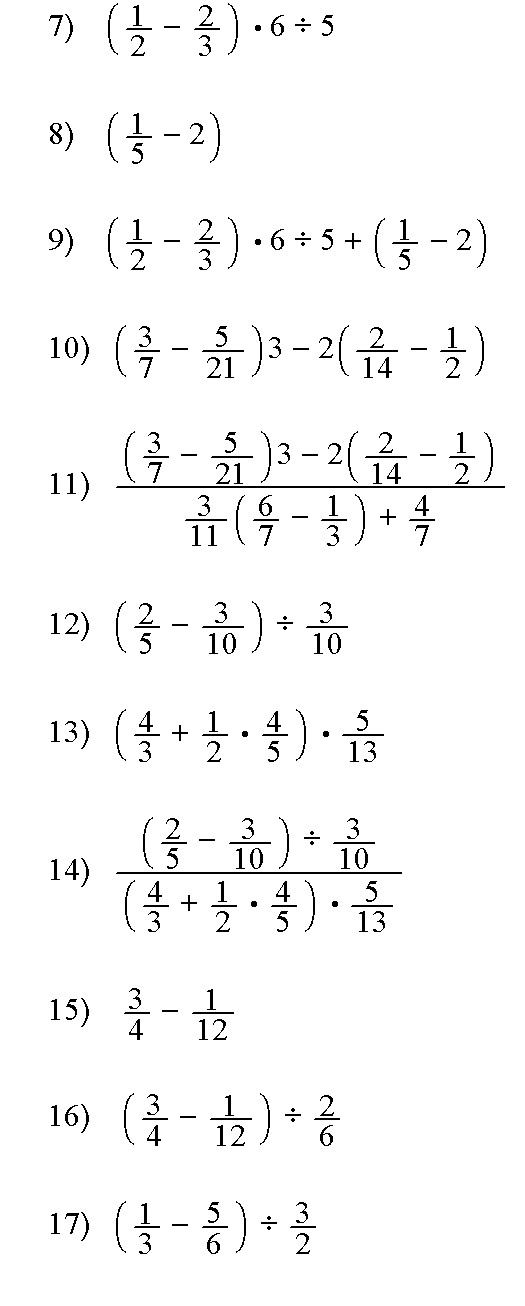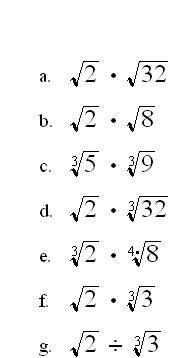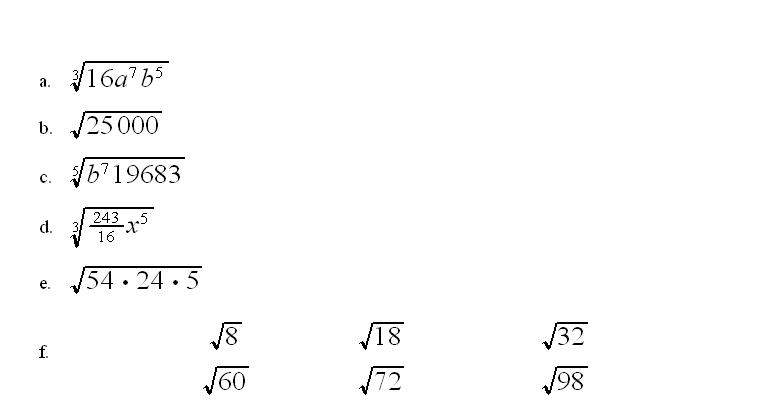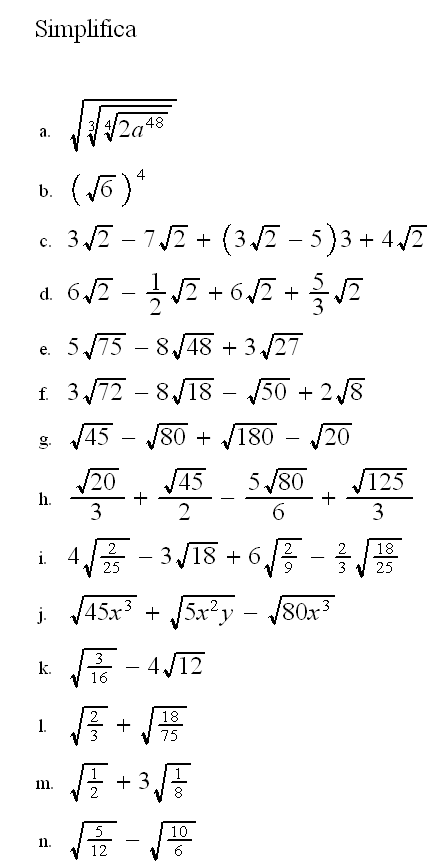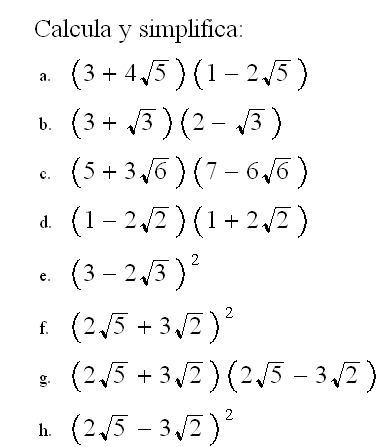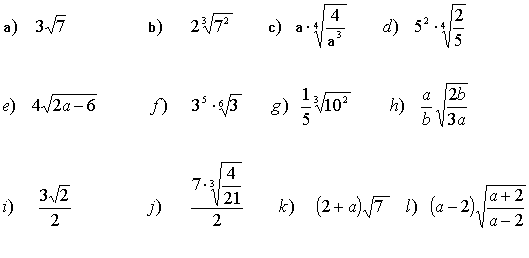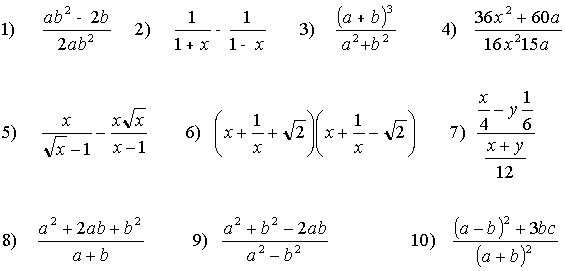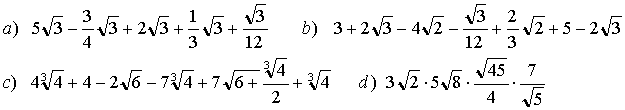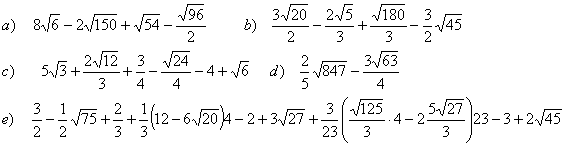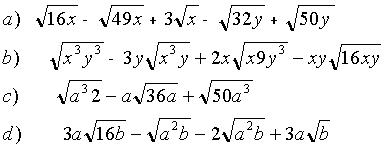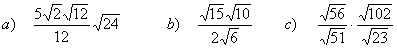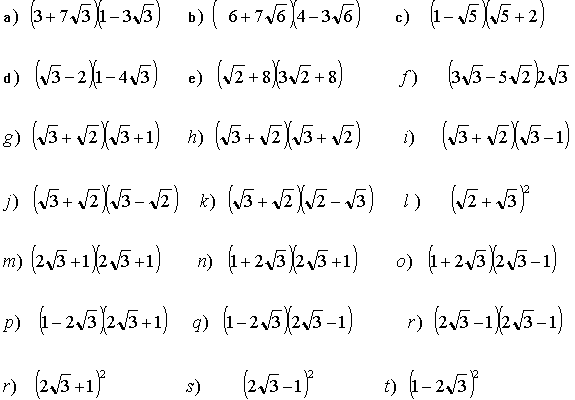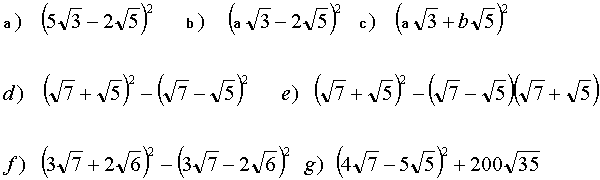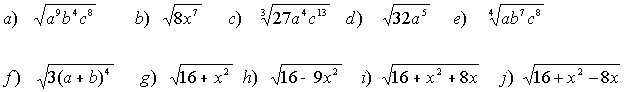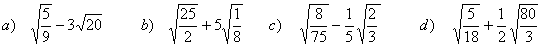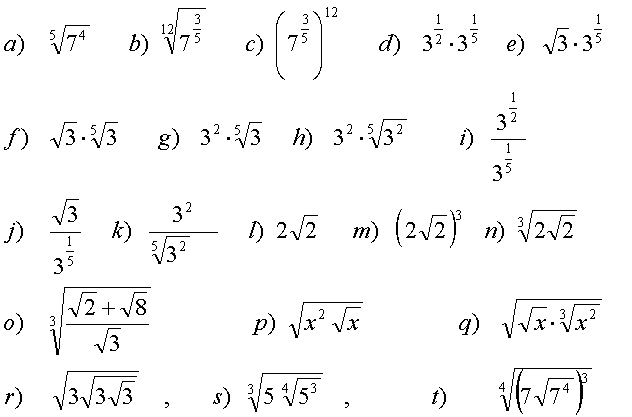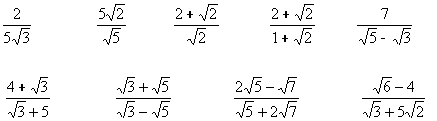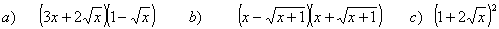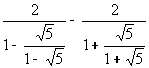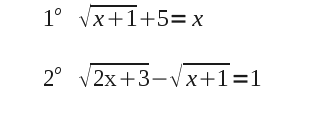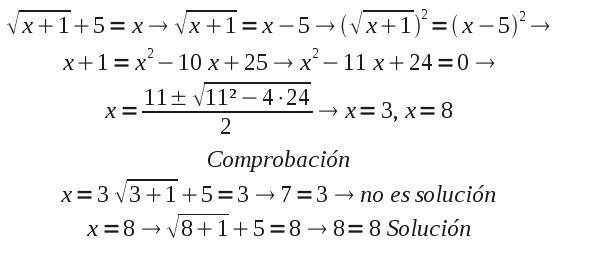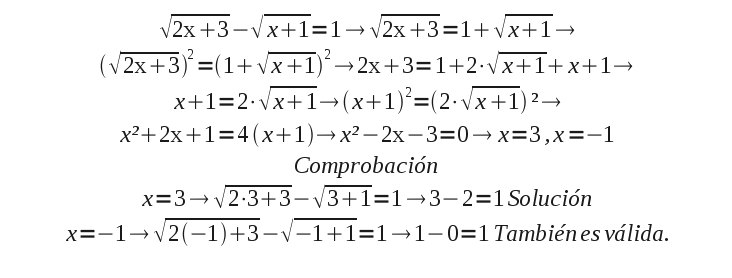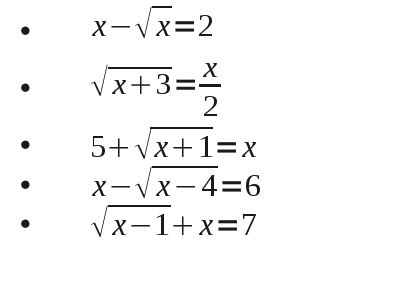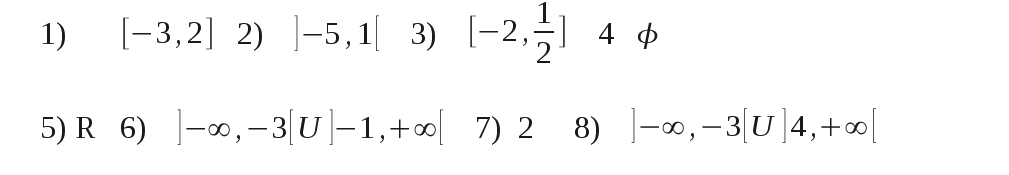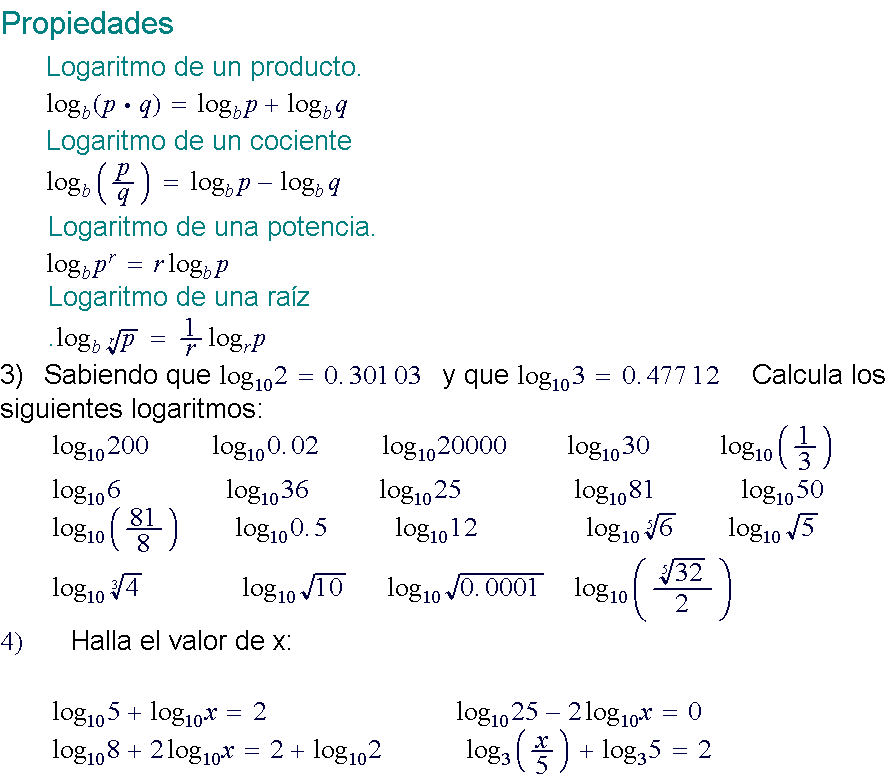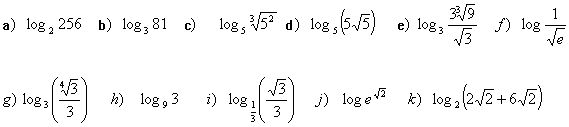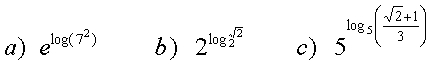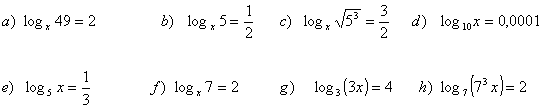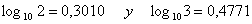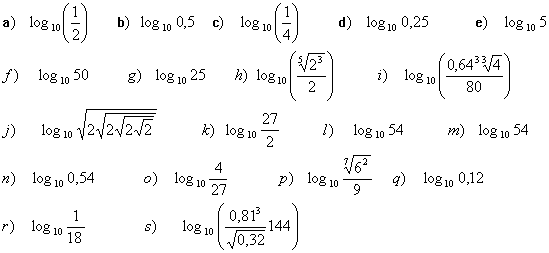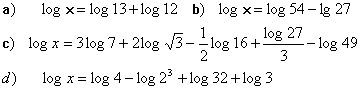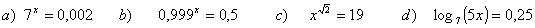Números Reales
Los números reales están formado por el conjunto de los números
fraccionarios, los que se pueden poner en forma de fracción junto con
los irracionales que son los que no admiten expresión fraccionaria.
Operaciones con fracciones
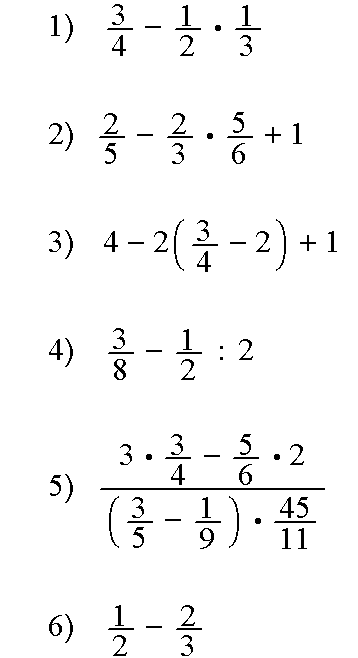
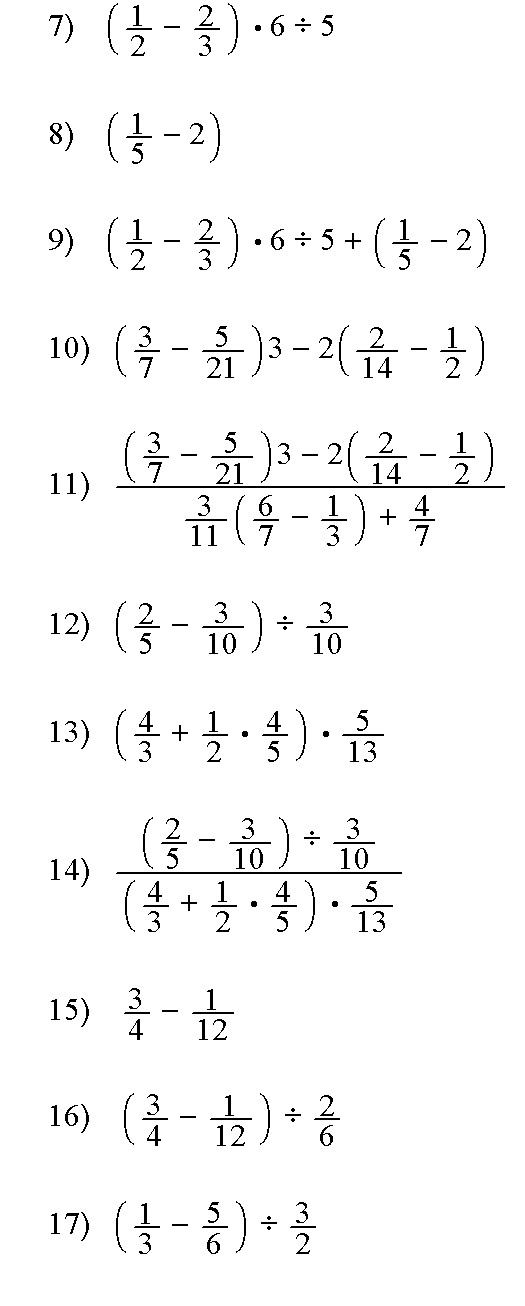
Introducción a los números reales
Números racionales:
Son
todos aquellos que se pueden poner en forma de fracción. Cualquier
número decimal con un número finito de cifras o con infinitas cifras
periódicas se puede poner en forma de fracción.
Halla una expresión decimal para las siguientes fracciones:


Encuentra las fracciones equivalentes para los siguientes números
decimales:


Dado los siguientes números :

Di cuáles son:
a) Reales
b) Irracionales
c) Racionales
d) Naturales
e) Enteros
Escribe las aproximaciones por defecto de los números:

para que el error cometido sea menor de:
Una décima
Una milésima
Escribe las aproximaciones por exceso de décima,
centésima y milésima de los números anteriores.
Recta Real
Podemos
dibujar una recta de forma que a cada número real le corresponda un
punto y al revés que a cada punto le corresponda un numero.

Representación de los números reales: Intervalos
Dado
un número cualquiera, podemos representar todos los números
reales
mayores que ese número por un intervalo abierto por los dos lados, por
medio de desigualdades o dibujándolos en la recta.

De
la misma forma se pueden representar los números comprendidos entre – 3
y 1, es decir los números más grandes que -3 y más pequeños que 1

Si en vez de estrictamente menor fuera menor o igual los extremos
pertenecen al intervalo y éste se llama cerrado.

También puede haber intervalos abiertos por la derecha y cerrados por
la izquierda y al revés.

Cuando uno de los extremos es infinito el intervalo siempre es abierto



Potencias con exponente fraccionario
Una raíz no es más que una potencia con exponente fraccionario escrita
de otra forma, por tanto tienen las misma propiedades que las potencias.
1 Calcula:

2 Halla el valor de x

Simplificar potencias:


3 Simplifica los siguientes radicales:

4 Escribe como potencias de exponente racional:

5) Halla el valor de las siguientes potencias:

Introducción de factores dentro de una raíz.
En
algunos casos cuando tenemos una raíz multiplicada por uno o varios
factores, nos puede interesar introducirlos dentro de la raíz. Para
ello elevamos los factores que queremos introducir al índice de la raíz
y lo ponemos dentro.
Ejemplos:
I)

II)

Extracción de factores en un radical
Es
el proceso inverso al anterior, para poder sacar factores de la raíz
estos tienen que estar elevado a un exponente mayor que el índice y se
descomponen en producto de factores con exponentes divisibles por el
índice. Para sacarlos se divide el exponente por el índice.

Multiplicación y divison de radicales
Si
tienen el mismo índice se multiplican o dividen los radicandos y se
queda el mismo índice. Del resultado se extraen fuera de la raíz los
factores que se puedan.

Si tienen distinto índice se transforman primero en radicales semejantes con índice común.

División de radicales:

Suma de radicales: No se pueden sumar lo único que podemos hacer es agrupar los que son iguales.

6 Expresa en forma de potencias de exponente entero positivo.

7 Calcula y simplifica:

8 Calcula
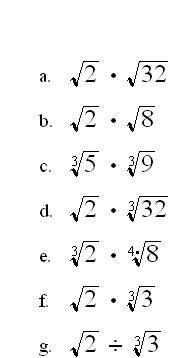
9-a Extrae factores fuera de la raíz
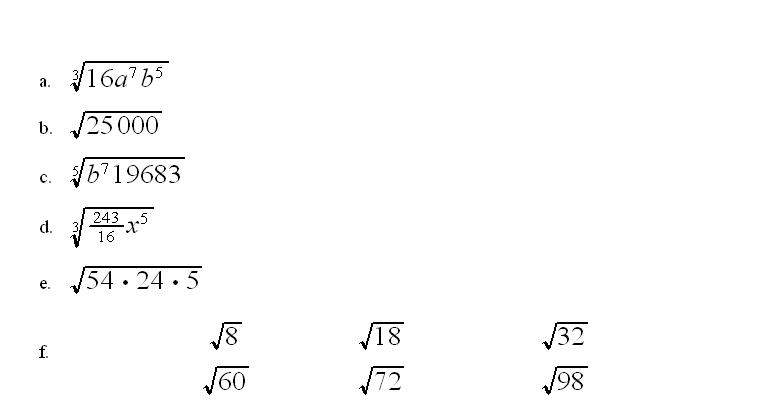
9-b
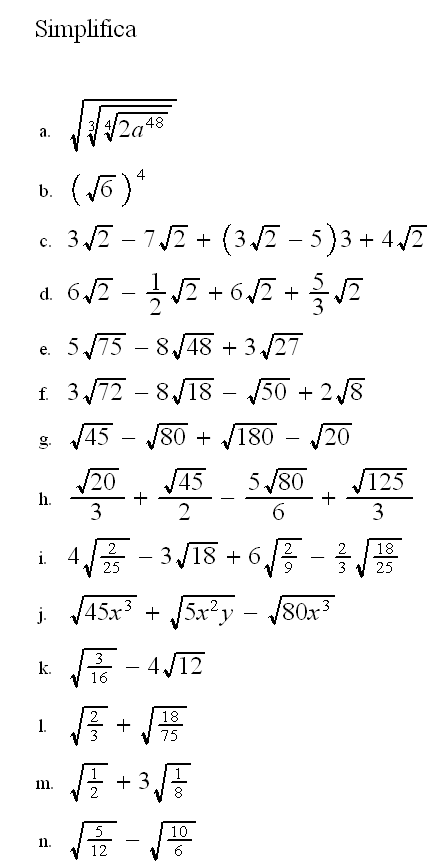
10
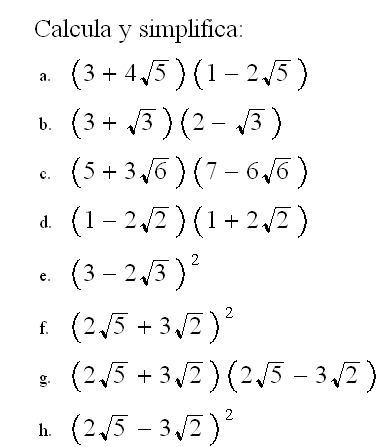
11 Introduce factores dentro de la raíz
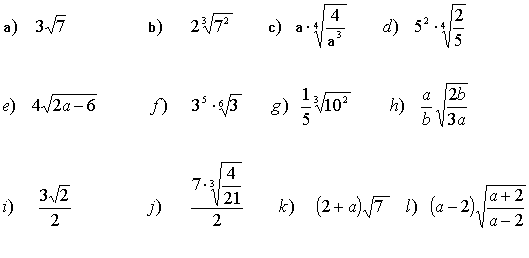
12 Simplifica todo lo que puedas
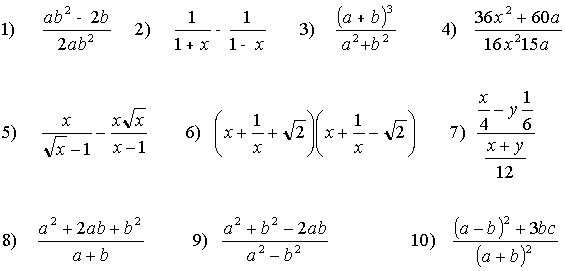
13 Calcula:
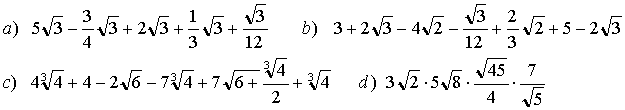
14 Calculad:
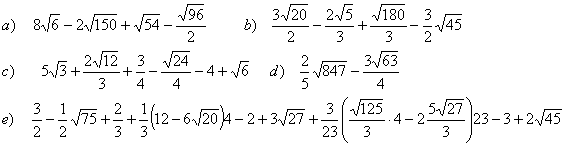
15
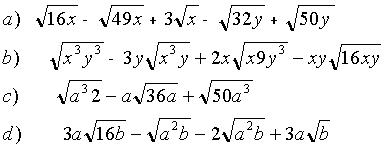
16
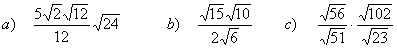
17
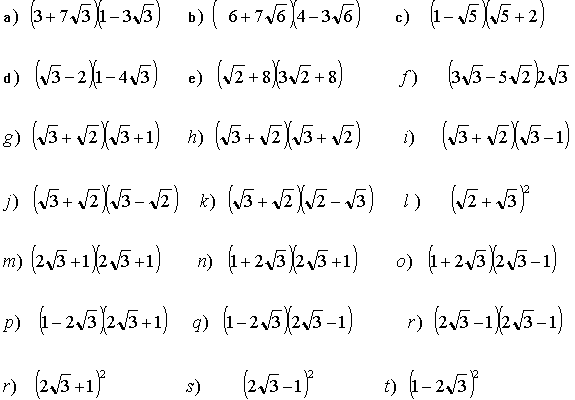
18
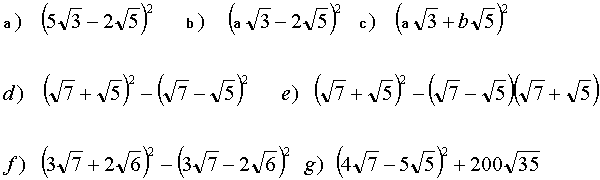
19 Extrae fuera de la raíz
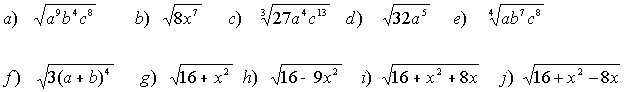
20 Calcula
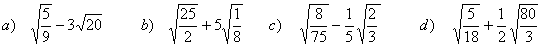
21 Escribe con exponente fraccionario.
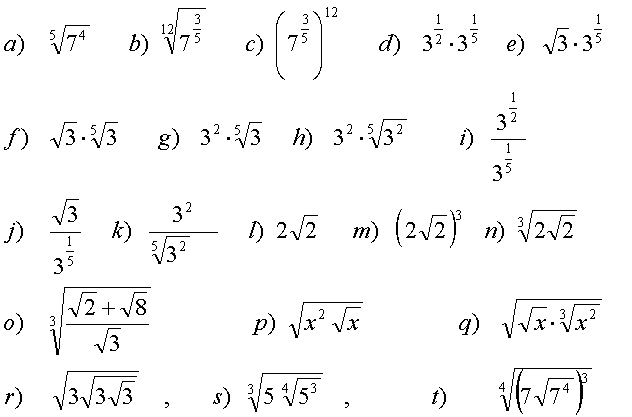
22 Racionaliza
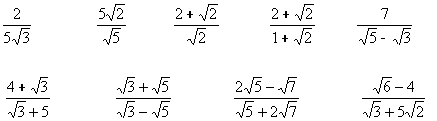
23 Simplifica
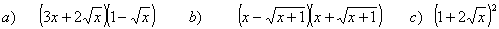
24
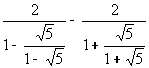

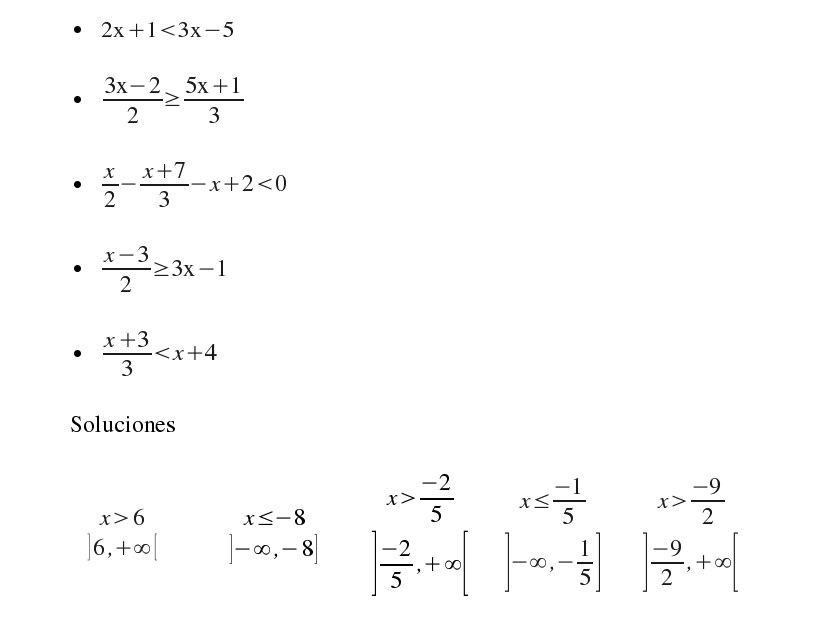
Inecuaciones primer grado
Logaritmos
Desarrollo histórico.
Los
logaritmos aparecen en matemáticas con el único fin de reducir en un
grado las operaciones y facilitar el trabajo de los calculistas. Su
principal propiedad es:

Llamamos logaritmo de un número a en una base determinada b al número que hay que elevar la base para que nos de el número a

Calcula a partir de la definición de logaritmo:

Halla el valor de x:

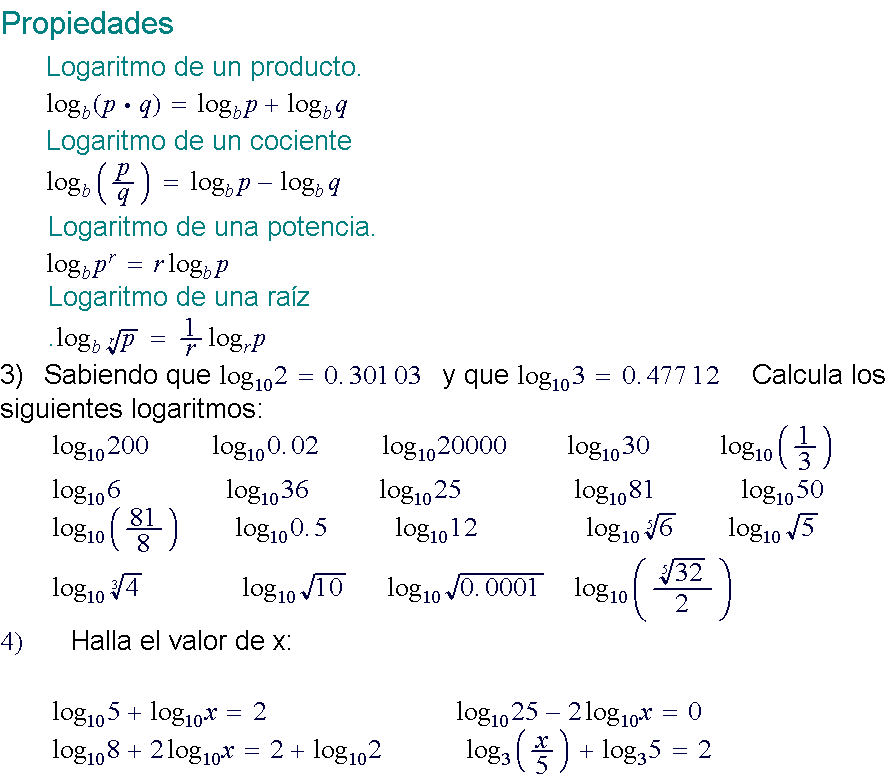

Ejercicios
1
Calcula:
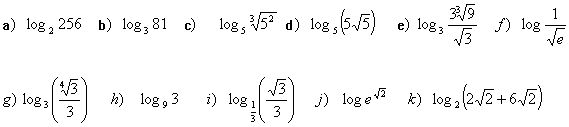
2
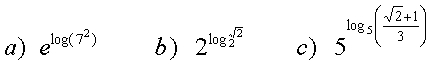
3 Halla el valor de x
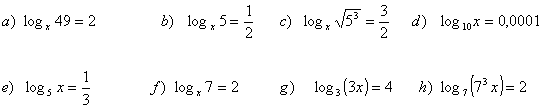
4
Sabiendo que :
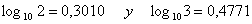
calcula:
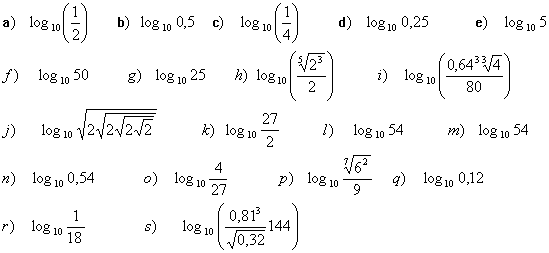
5
Halla el valor de x
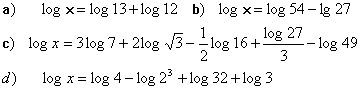
6
Halla el valor de x con ayuda de la calculadora
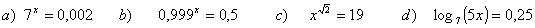
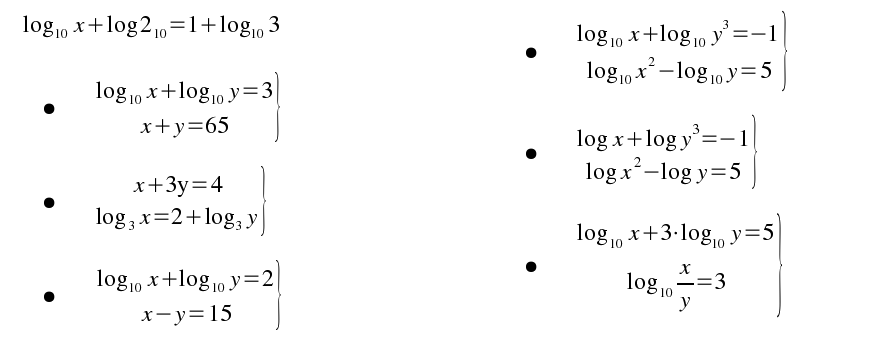
Ecuaciones exponenciales y logarítmicas
1
Halla el valor de x

2 Resuelve y comprueba el resultado:

3 Halla el valor de x

5 Resuelve y comprueba el resultado