

» 3 ¿Cuántos litros de leche con 35% de
grasa han de mezclarse con leche de 4% de grasa para obtener 20 litros
al 25% de grasa.


» 6 Cuatro hermanos tienen 45 €. Si el dinero del primero se aumenta en 2 €, el del segundo se reduce en 2 €, el del tercero se duplica y el del cuarto se reduce a la mitad, todos los hermanos tendrán la misma cantidad de €. ¿Cuánto dinero tenía cada uno?
» 7 Una campesina llegó al mercado a vender huevos. La primera clienta le compró la mitad de todos los huevos más medio huevo. La segunda clienta adquirió la mitad de los huevos que le quedaban más medio huevo. La tercera clienta sólo compró un huevo. Con esto terminó la venta, porque la campesina no tenía más huevos. ¿Cuántos huevos llevó al mercado la campesina?

» 8 Un padre, al morir, dejó establecido que el hijo mayor recibiría 10000 €. más la quinta parte del resto. El siguiente 20000 €. más la quinta parte del nuevo resto. Y en la misma forma cada hijo iría recibiendo 10.000 € más que el anterior y la quinta parte del resto. Al final todos recibieron igual cantidad. ¿Cuántos herederos había y qué cantidad recibió cada uno?
Para resolverlo calcular lo que le corresponde a los dos primeros hijos.
» 8 La señora Justa compró un cierto número de huevos, por los que pagó 6 €. Al volver a casa se le cayó la cesta rompiéndosele 2 huevos, con lo que el precio le resultó 1,2 €. más caro por docena, con respecto al que pagó inicialmente en el supermercado. ¿Cuántos huevos compró la señora Justa?
» 10 Para que aprendiera matemáticas la madre de Alejandro le puso 26 problemas. Por cada ejercicio resuelto correctamente le daría 3 € y por cada ejercicio no resuelto Alejandro le daría uno a su madre. Alejandro terminó ganando 62 € ¿Cuántos ejercicios resolvió?
» 11 Antonio ha comprado 5 bolígrafos y 4 cuadernos por 7€ Luis ha pagado 4,6 €. por 3 bolígrafos y 4 cuadernos. ¿Cuánto vale un bolígrafo y un cuaderno?
» 12 Cincuenta y seis raciones de pienso han de servir de comida a diez animales; cada animal es un perro o un gato. Cada perro ha de obtener seis raciones y cada gato, cinco. ¿Cuántos perros y cuántos gatos hay?
» 13 Manolo compro una entrada de fútbol rebajada en un 10%. Posteriormente la vendió en la reventa por un 20% más de lo que a él le costo. Sabiendo que el comprador consiguió la entrada por 4,8 € más de su precio real. ¿Cuál era este?
» 14 Cierta tienda de animales vende loros y periquitos; cada loro se vende a dos veces el precio de un periquito. Entró una señora y compró cinco loros y tres periquitos. Si en vez de eso hubiese comprado tres loros y cinco periquitos habría gastado 20 dólares menos. ¿Cuál es el precio de cada pájaro?
» 15 Tres docenas de limones cuestan tantos duros como limones dan por 16 duros. ¿Cuánto vale la docena de limones?
» 16 Un granjero tenía algunas tierras. Un tercio lo destinaba al cultivo del trigo, un cuarto al cultivo de guisantes, un quinto al cultivo de judías, y en las veintiséis hectáreas restantes cultivaba maíz. ¿Cuántas hectáreas tenía en total?
» 17 Cierto día Ana estaba atendiendo a 30 invitados. Tenía 100 pasteles para repartir entre ellos. En lugar de cortar ningún .pastel a trozos, decidió dar 4 pasteles a cada uno de los invitados preferidos, y tres a cada uno de los demás invitados. ¿Cuántos eran sus invitados preferidos?



4) Se pusieron dos a jugar con otros y ambos perdieron el uno 12 reales, y el otro 57 reales: el dinero con que éste segundo se levantó del juego era la cuarta parte del que al primero le había quedado, siendo así que los dos se pusieron a jugar con igual cantidad de dinero. ¿Cuál era esta cantidad?

5) Preguntándole a uno qué edad tenía un hijo suyo, respondió: si del doble de su edad se resta el triple de la que tenia 6 años ha resultará su edad actual ¿Cuántos años tenia el hijo?
6) Siendo en un reloj las 12 en punto y estando por consiguiente el minutero sobre el horario, ¿qué hora será cuando el minutero vuelva a colocarse sobre el horario?
7) Dispuso uno en su testamento que del capital que dejaba se diesen al mayor de sus hijos 1000 duros y la décima parte del resto, que al hijo segundo se diesen 2000 duros y la décima parle del resto al tercero, 3000 duros y la décima parle del resto y así sucesivamente. Hecho el reparto se vio que todas las partes eran iguales. ¿Cuánta era toda la herencia, cuántos eran los hijos y cuánto correspondió a cada uno ?
8) Una liebre perseguida por un algo se halla a 60 saltos suyos distante del galgo: la liebre da 3 saltos mientras el galgo da 2, pero 3 saltos del galgo equivalen a 7 de la liebre . ¿Cuántos saltos dará la liebre hasta que la alcance el galgo y cuántos el galgo para avanzar a la liebre?
9) Teniendo 16 libras de pólvora a 12 reales ¿cuántas libras de a 8 reales se deberán juntar con ellas para que cada libra de la mezcla valga diez reales y medio?
12) En una sala hay tres estatuas de Juno Júpiter y Febo tales que las dos primeras pesan veinte minas (o arrobas), y la tercera que pesa seis, es igual a la cuarta parte de la primera, mas la tercera parte de la segunda; ¿Cuánto pesa cada una?
13) Edad de Alejandro
Preguntaba Diodoro
Embajador del príncipe de Egipto,
Qué edad tenía el Macedon invicto:
Y luego Artemidoro
Le responde ingenioso:
Dos años tiene mas el belicoso
Rey que su camarada
Efestion, cuyo padre
cuatro mas que los dos enumeraba,
y el padre de Alejandro
cuando noventa y seis giros de Apolo
Los años de estos tres contaba solo.
14) Estando Hércules interesado en quitarle las vacas a Augeo, rey de los eleos, le preguntó cuántas tenía. Esta fue la respuesta.
Hércules vino a visitar á Augéo,
que era muy opulento
y teniendo deseo de robarle sus vacas ciento a ciento
pregunta con cuidado
el número y lugar de su ganado.
Yo señor, dice el venerable anciano,
brevemente respondo:
que en aquel rico llano
cuya orla es oro y esmeralda el fondo
a la margen de Alféo
La mitad de mis vacas pacer veo;
la octava parte de Saturno el monte
turba con sus bramidos
y en distante horizonte
la duodécima tiene destruidos
los valles que es muy fiera;
en el monte, en el prado, en la ribera
la vigésima parte.
En Elide segura se apacenta
De Arcadia ya se aparta
la trigésima; y corren por mi cuenta
cincuenta cuyas voces
hoy son suaves y mañana atroces.
Mover la clava pero no la pluma
sabe el hijo de Alcmena
y así se queda sin saber la suma
del ganado que, en los montes suena,
tu que eres mas experto
el número descubre que he encubierto
15)

Para hallar la fórmula general:




» 14 Un poste tiene bajo tierra tres octavos de su longitud, tres quintos del resto sumergido en agua y sobresale del agua 4 m. ¿Cuál es la longitud del poste?
» 15 Un padre tiene 70 años y su hijo la mitad. ¿Cuántos años hace que el padre tenía la edad del hijo?
» 16 Uno dice que su edad es igual al doble de los años que tiene menos el triple de los que tenía hace seis años. ¿Cual es su edad?
» 17 Reparte 578 en partes inversamente proporcionales a 4, 6 y 18
» 18 Un depósito tiene un grifo que lo llena en 3 horas, otro en 4 y un desagüe que lo vacía en 5 horas. ¿Cuánto tiempo tardaría en llenarse con todo abierto?
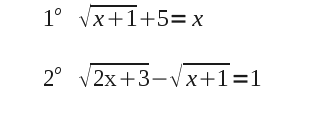
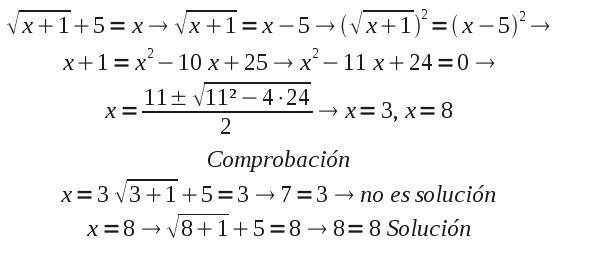
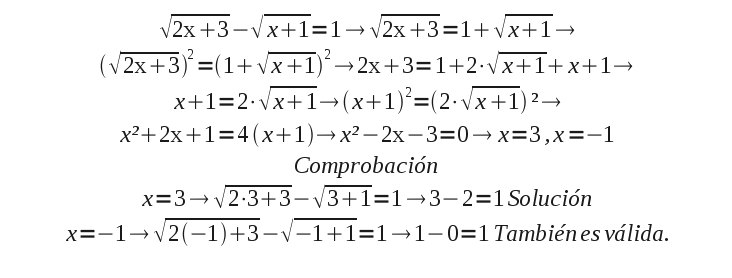
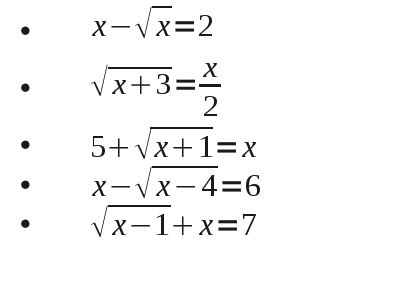
Una inecuación es una desigualdad algebraica con al menos una variable o incógnita.
Resolver una inecuación es encontrar todos los valores de las variables que hacen cierta la desigualdad.
Resolución de inecuaciones con una incógnita.
Una inecuación de primer grado se resuelve igual que una ecuación con la única diferencia que si multiplicamos los dos miembros de la inecuación por un mismo número negativo la desigualdad cambia de sentido.
Ejercicios
Solución todos los números reales menores o iguales que 4
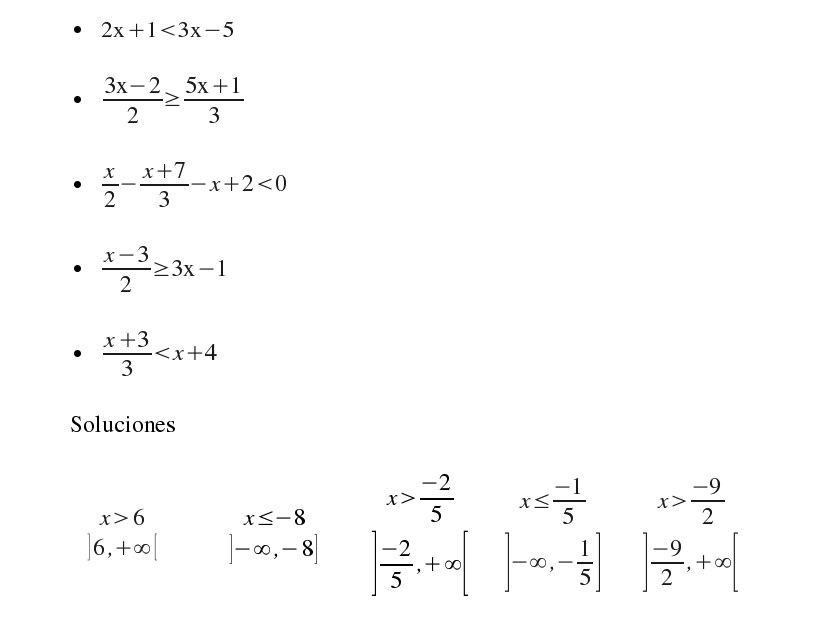
Solución:
Para que se cumplan las dos desigualdades los valores de x tendrán que estar comprendidos entre -5 y 1.
Será menor o igual que 0 en:

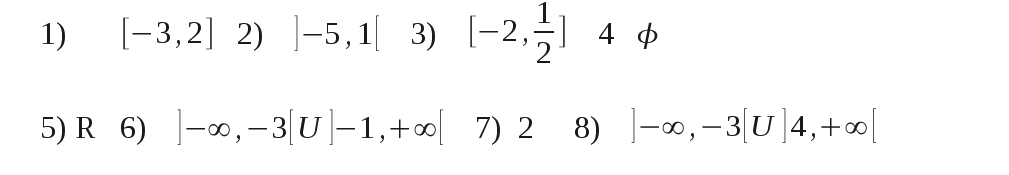
Solución:
No podemos multiplicar por el denominador sin tener en cuenta la variación del signo para los distintos valores de x, parece más simple agrupar todos los valores en una fracción:
El numerador se hace cero para x = -2 y el denominador para x = 1/3
Solución:
El numerador se anula en x=2 y x=-2 y el
denominador en x= 4
El 4 es abierto porque no puede ser 0 el denominador.