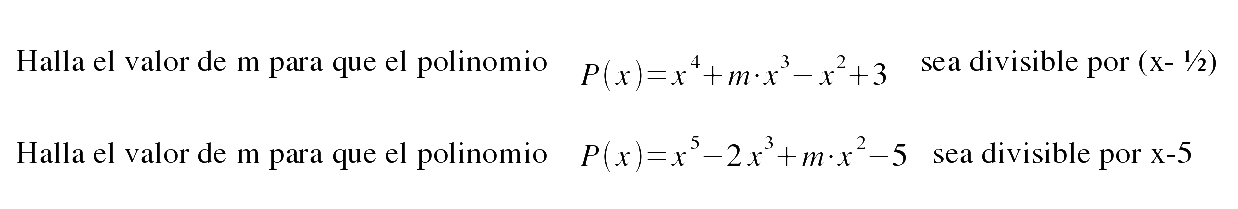Fórmulas
Empecemos con un problema:
Nos dan la suma y la diferencia de dos números y nos piden hallad ambos, podemos resolver el problema para este caso concreto o encontrar una fórmula que nos permita utilizarlo para cualquier par de números.
Siendo conocidas la suma y diferencia de dos números, hallad cada uno de ellos.
Si
el menor de los números fuese conocido x, sumándole la diferencia
hallaríamos el mayor. Representamos por s la suma, por d la diferencia,
por x el menor y por y el mayor.
Para hallar el mayor sumar la diferencia a la suma y dividir por dos el resultado. Es obvio que es preferible las expresiones de los recuadros que no los dos últimos párrafos.
Otro ejemplo:
Tenemos dos grifos para llenar un estanque tales que el primero arroja b litros por minuto y el segundo c. . El segundo ha permanecido abierto d minutos más que el primero: ¿Cuánto tiempo ha estado abierto cada grifo.?Llamemos x al tiempo que ha estado abierto el primer grifo; el tiempo que ha permanecido el segundo será d+ x
Una ecuación es una expresión con una igualdad entre dos cantidades, de las cuales, al menos una contiene una o varias incógnitas. En álgebra los problemas se representan por ecuaciones, los números que se buscan, las incógnitas, se representan por letras, los conocidos por cifras o también letras si se busca una expresión mas general.
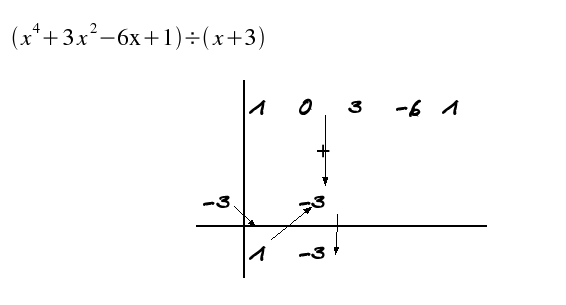
Primer paso -3 · 1= -3 → 0 + -3 = -3
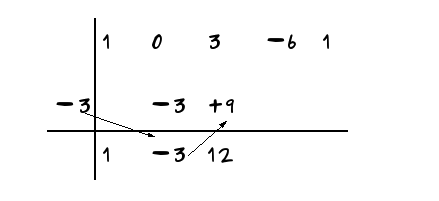
Segundo -3 · (-3) = +9 → 3 + 9 = 12

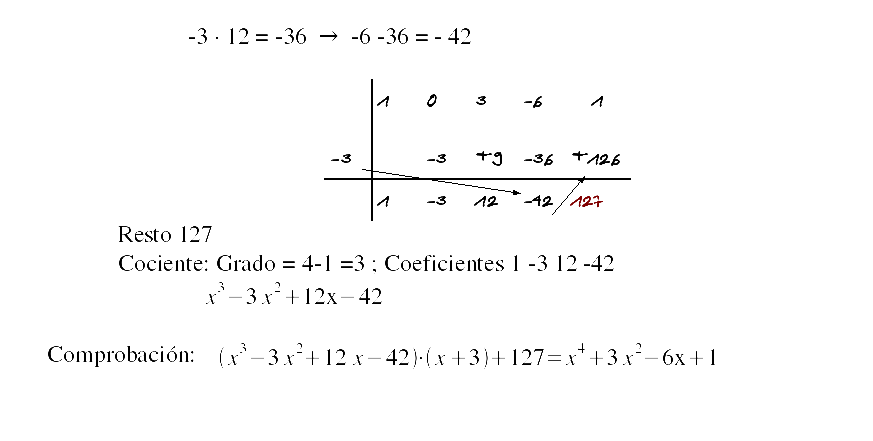

Soluciones:
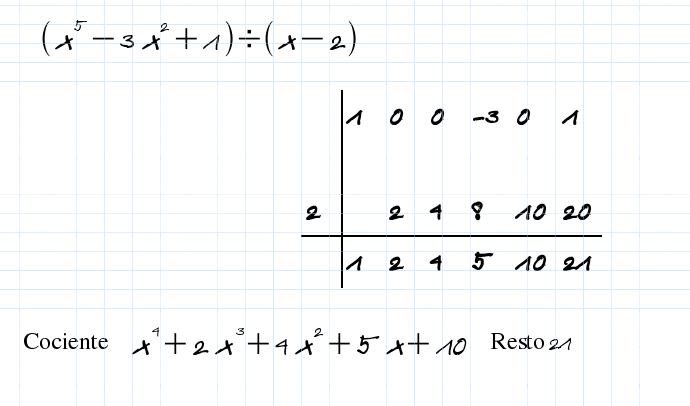
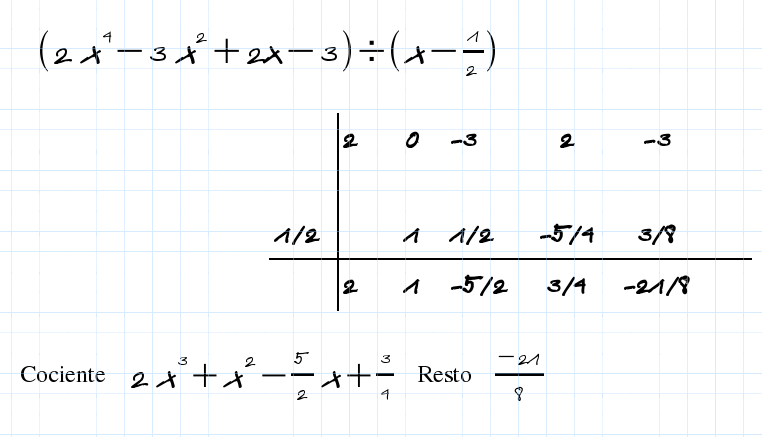
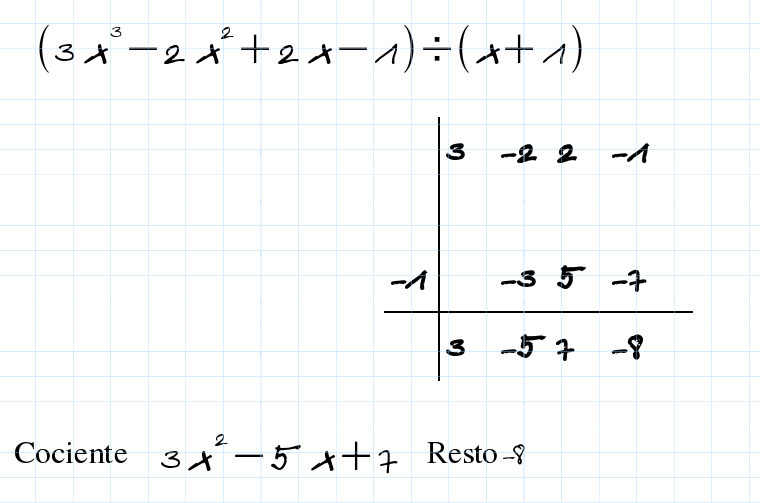
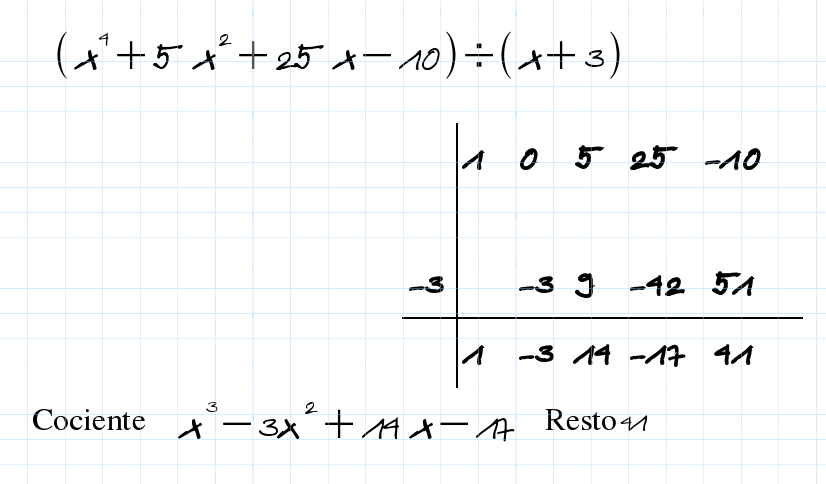
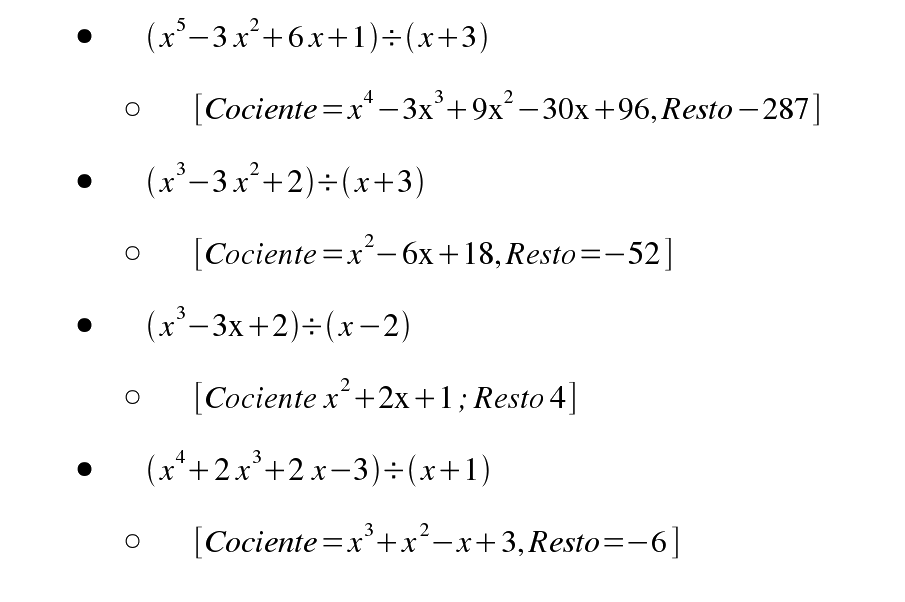
El valor numérico P(a) de un polinomio P(x) para x=a coincide con el resto de dividir el polinomio P(x) por x-a .
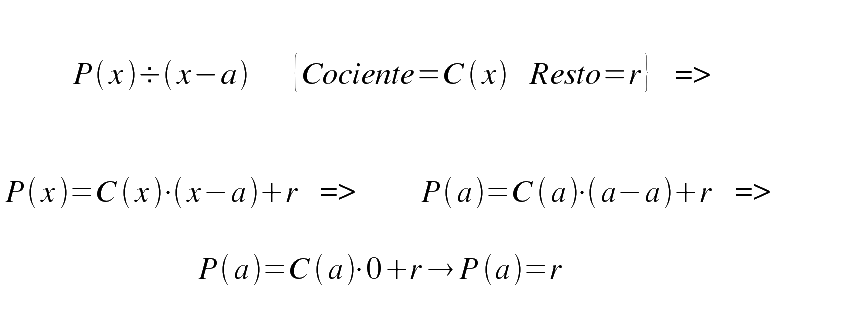
Raíces o ceros de un polinomio son aquellos valores de x para los cuales el valor numérico es cero.
Para que x=a sea una raíz del polinomio P(x) este tiene que ser divisible por x-a