Álgebra y geometría
Programación lineal 1
Programación
lineal .
Problemas
1)
2)
3)
4)
5)
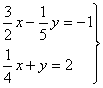
6)
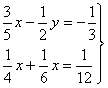
7)
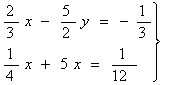
8)
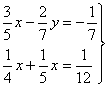
9)
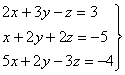
10)
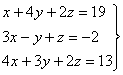
11)
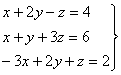
12)
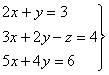
13)
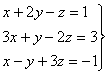
14)
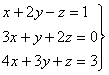
15)
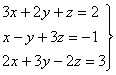
16)
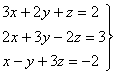
18)
19)
20)
22)
23)
24)
25)
26)
27)
28)
29)
30)
31)
32)
33)
34)
1) Dada la matriz M
∙∙∙
a)
Haya los elementos: 
para
i=1 , 2 , 3, 4
b)
Los elementos 
para j=1, j=2;
j=3 j=5
_________
2) Dadas las matrices:
Hallad las matrices: A+B; A-B ; A+2B ; 3A-2B
_________
3) Dadas las matrices cuadradas:
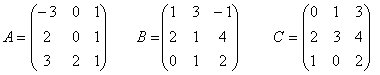
a) Escribe los elementos de la diagonal principal de cada una de las matrices.
b) Calcula: A+2B
c) A+BT
d) 2AT+B
e) A+B-C
f) A-(B+C)
g) –A-B-C
h) A∙B
i) B∙A
_________
4) Dadas las matrices A yB:
a)
Hallad la matriz 3A+2B
b)
Hallad las matrices X e Y para que se cumpla:
_________
5) Dadas las matrices:
Calculad: A∙(B∙C) ; (A∙B)∙C ; (A∙C)∙B
_________
6) En un taller se fabrican tres tipos de productos A, B y C. Las horas de trabajo necesarias para cada uno son 50, 70 y 110 respectivamente. Las cantidades de unidades de material son 80, 120 y 250 . Y las unidades de servicios ajenos son: 30, 20 y 80. La hora de trabajo cuesta 20 €, la unidad de material 5€ y la unidad de servicios 8€. Hallad el coste de fabricación de 1000 unidades de A, 500 de B y 1500 de C.
_________
7) Hallad la matriz inversa de las siguientes matrices:
_________
8) Hallad la matriz inversa de las siguientes matrices:
_________
9) En un centro de enseñanza utilizan el transporte escolar alumnos del centro urbano C y de dos urbanizaciones Ay B. En 1º hay matriculados 80 alumnos de C, 20 de A y 30 de B. En 2º 70 de C, 15 de A y 20 de B. En 3º 60, 40 y 15 respectivamente. En 4º 50, 20 y 12. El coste del transporte por alumno y año se estima en 100€ para los alumnos del centro urbano, 120€ para los de la urbanización A y 140€ para los de B. Expresar por medio de un producto de matrices el coste total del transporte escolar.
_________
10) Dada una matriz A ¿existe una matriz B, tal que el producto AB o BA sea una matriz de una sola fila.?. Poner un ejemplo para una matriz 3X4.
_________
11)
Dada la matriz 
Hallad
_________
12) Calculad x , y , z , t para que se cumpla:
_________
13) Dadas las matrices:
Hallad una matriz X que cumpla: 3X-2A=5B
_________
14) Calculad:
_________
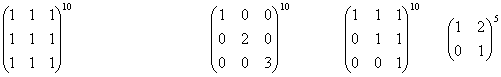
15) Dada la matriz A:
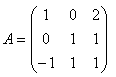
Hallad: 
_________
16) Calculad la matriz inversa:
_________
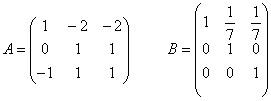
17)
Sea una matriz A que verifica: 
Hallad
;
_________
18) Hallad el rango de forma razonada de:
_________
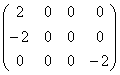
19) Dadas las matrices:
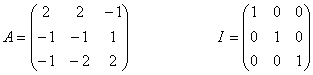se pide:
1)
Calcular la matriz .
2)
Haciendo uso del apartado anterior hallar 
20) Si P y Q son dos matrices cuadradas de orden n ¿es cierta en general la igualdad :
_________
21) Dada la matriz:
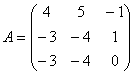
Calculad 
_________
22) Un fabricante produce tres tipos de clavos: de aluminio (A), de cobre (Q) y de acero (H). Todos ellos se fabrican en longitudes de 1; 1,5 ; 2 y 2,5 centímetros con los precios respectivos siguientes :
Clavos A: 0,20 0,30 0,40 0,50 pts
Clavos Q 0,30 0,45 0,60 0,75 pts
Clavos H 0,40 0,60 0,80 1pts.
Sabiendo que en un minuto se producen:
De 1 cm de longitud: 100 A 50 Q 700 H
De 1,5 cm de longitud 200 A 20 Q 600 H
De 2cm 500 A 30 Q 400 H
De 2,5 cm. 300 A 10 Q 800 H
Se pide:
Resumir la información anterior en dos matrices M, y N. M será un matriz 3x4 que recoja la producción por minuto y N una matriz 4X3 que recoja los precios.
Calcular los elementos de la diagonal principal de la matriz MN y dar su significado.
Hacer lo mismo para NM
_________
23) Calculad:
_________
24) Calculad:
_________
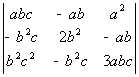
25) Resolver sin desarrollar, aplicando y justificando las propiedades utilizadas de los determinantes:
_________
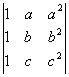
26) Sabiendo que:
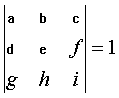y
utilizando correctamente las propiedades de los determinantes, calcular:
_________
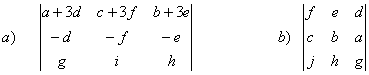
27) Dada la ecuación:
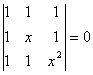
Sin desarrollar el determinante hallar dos soluciones de la ecuación dada.
_________
28) Sin desarrollarlo demostrar que el siguiente determinante es igual a cero:
_________
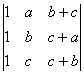
29) Dada la siguiente matriz, averiguar vara que valores de m tiene inversa y calcular ésta para m=2.
_________
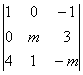30) Hallar una matriz X tal que:
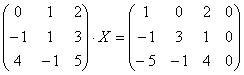
31) En la sala de un hospital dedicado al tratamiento de diabéticos se administra insulina de tres clases: semilenta, lenta y ultralenta. El número de unidades diarias que se aplica a los pacientes de los cinco ingresados viene dado por la siguiente tabla:
|
|
Paciente 1 |
Paciente 2 |
Paciente 3 |
Paciente 4 |
Paciente 5 |
|
Semilenta |
15 |
15 |
20 |
30 |
10 |
|
Lenta |
20 |
20 |
15 |
5 |
20 |
|
Ultralenta |
10 |
5 |
10 |
10 |
15 |
El número de días que ha estado internado cada paciente es:
|
|
Paciente 1 |
Paciente 2 |
Paciente 3 |
Paciente 4 |
Paciente 5 |
|
nº de días |
3 |
7 |
7 |
12 |
20 |
Calcula con ayuda del producto de matrices, las unidades de cada clase que le fue administrada a los pacientes.
32)
En un hospital oncológico se aplica a un grupo de cuatro pacientes un tratamiento de quimioterapia mediante un protocolo CMF (C = ciclosfamida, M=metrotexate, F= fluoracilo). Las cantidades diarias que necesita cada paciente de cada uno de los compuestos varían según la superficie corporal total del siguiente modo:
Paciente 1 : 1200 mg de C, 80 mg de M y 1200 mg de F
Paciente 2: 900 mg. de C, 60 mg. de M y 950 mg. de F
Paciente 3: 1100 mg. de C. 70 mg de M y 1000 mg de F.
Paciente 4 1150 mg de C, 80 mg de M y 1100 mg de F
Teniendo en cuenta que el tratamiento se va a aplicar durante tres semanas a los pacientes 1, 3, y 4 y dos semanas al paciente 2, hallar la matriz de necesidades diarias y las cantidades de cada compuesto necesarias para poder atender correctamente los tratamientos de los cuatro pacientes.
33)
a) El determinante de un sistema de igual número de ecuaciones que de incógnitas es 0. ¿Puede ser el sistema compatible? ¿Es incompatible? Razonar las respuestas con un ejemplo.
b) En un sistema de ecuaciones lineales det(M) = 0, ¿puede tener solución el sistema? ¿Se puede aplicar la regla de Cramer? Razonar la respuesta.
c) El rango de la matriz de los coeficientes de un sistema de tres ecuaciones con tres incógnitas es 1. ¿Qué rango puede tener como máximo la matriz ampliada? Razonar la respuesta,
d) Un sistema de dos ecuaciones con dos incógnitas es homogéneo y el rango de la matriz de los coeficientes es 2. Si se interpretan las ecuaciones como rectas, ¿tienen algún punto en común? ¿Cuál es? Razonar las respuestas geométrica mente.
e) Si el rango de la matriz de los coeficientes de un sistema de tres ecuaciones con tres incógnitas es 2, ¿puede ser compatible el sistema? ¿Puede ser compatible y determinado? ¿Puede ser incompatible? Razonar las respuestas, a poder ser con ejemplos concretos.
Un sistema de tres ecuaciones lineales con dos incógnitas, ¿puede ser compatible y determinado? En caso afirmativo, dar un ejemplo.
Programación lineal
Inecuaciones y sistemas de inecuaciones
Resolver las siguientes inecuaciones
1) 2x-y ≥ x-3y-6 4) x≤4 7) 0,3x+0,4y≥ 12
2) x + 3y ≤ 1 5) y<8 8) x<0
3) 2x-5y>2 6) 0,5 x - 0,25 y ≤ 2 9)y-x≤0
Resuelve los siguientes sistemas de inecuaciones
4)
x>0 x≥0
y<0 y>0
4x + y<16 4x + y<16
y ≤ 8 4x + 3y ≤12
4x + y ≤20 x + 2y ≤ 6
x + 2y ≤12 x + y ≤5
x ≥ 0 , y ≥ 0
5) x + y ≥ 3 x + 4y ≤ 2 x + 2y -1 ≥ 0
2x-y ≤ 0 x + 4y ≥ 4 2x + y ≤ 0
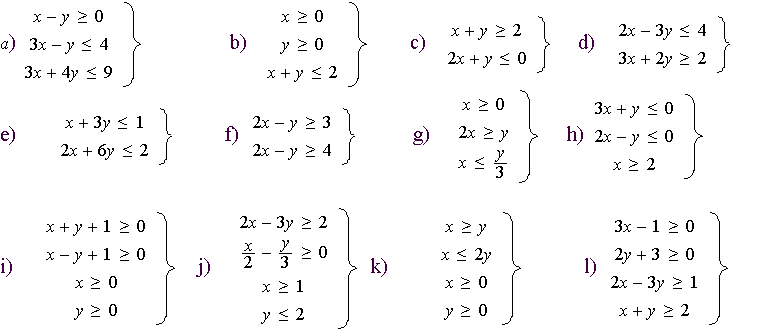
Programación lineal
1 Un estudiante dedica parte de su tiempo al reparto de propaganda publicitaria. La empresa Ale paga 5 Ptas. por cada impreso repartido y la empresa B, con folletos más grandes, le paga 7 pesetas por impreso. El estudiante lleva dos bolsas: una para los impresos A, en la que caben 120, y otra para los impresos B, en la que caben 100. Ha calculado que cada día es capaz de repartir 150 impresos como máximo.
Lo que se pregunta el estudiante es: ¿cuántos impresos habrá de repartir de cada clase para que su beneficio diario sea máximo?
2) En una fábrica de bombillas se producen dos tipos de ellas, las de tipo normal valen 450 pesetas y las halógenas 600 pesetas. La producción está limitada por el hecho de que no pueden fabricarse al día más de 400 normales y 300 halógenas ni más de 500 en total. Si se vende toda la producción, ¿cuántas de cada clase convendrá producir para obtener la máxima facturación?
3 Una compañía aérea tiene dos aviones A y B para cubrir un determinado trayecto. El avión A debe hacer más veces el trayecto que el avión B pero no puede sobrepasar 120 viajes. Entre los dos aviones deben hacer más de 60 vuelos pero no menos de 200. En cada vuelo A consume 900 litros de combustible y B 700 litros. En cada viaje del avión A la empresa gana 300000 Ptas. y 200000 por cada viaje del B. ¿Cuántos viajes debe hacer cada avión para obtener el máximo de ganancias? ¿Cuántos vuelos debe hacer cada avión para que el consumo de combustible sea mínimo?
3) Una fábrica de carrocerías de automóviles y camiones tiene dos naves. En la nave A, para hacer la carrocería de un camión, se invierten 7 días-operario, para fabricar la de un coche se precisan 2 días-operario. En la nave B se invierten tres días operario tanto en carrocerías de camión como de coche. Por limitaciones de mano de obra y maquinaria, la nave A dispone de 300 días operario, y la nave B de 270 días-operario. Si los beneficios que se obtienen por cada camión son de 6 millones de pesetas y por cada automóvil 2 millones de pesetas, ¿cuántas unidades de cada uno se deben producir para maximizar las ganancias?
4) Un pastelero tiene 150 Kg. de harina, 22 Kg. de azúcar y 27'5 Kg. de mantequilla para hacer dos tipos de pasteles P y Q Para hacer una docena de pasteles de tipo P necesita 3 Kg. de harina, 1 Kg. de azúcar y 1 de mantequilla y para hacer una docena de tipo Q necesita 6 Kg. de harina, 0'5 Kg. de azúcar y 1 Kg. de mantequilla. El beneficio que obtiene por una docena de tipo P es 20 y por una docena de tipo Q es 30. Halla, utilizando las técnicas de programación lineal, el número de docenas que tiene que hacer de cada clase para que el beneficio sea máximo.
5) Una empresa fabrica dos tipos de rotuladores, de la clase A 200 Ptas. la unidad y de la clase B a 150 Ptas. En la producción diaria se sabe que el número de rotuladores de la clase B no supera en 1000 unidades a los de la A; además, entre las dos clases no superan las 3000 unidades y la de la clase B no bajan de 1000 unidades por día. Hallar el costo máximo y mínimo de la producción diaria.
6 Una compañía fabrica dos modelos de sombrero: Bae y Viz. La fabricación de los sombreros se realiza en las secciones de moldeado, pintura y montaje. La fabricación de cada modelo Bae requiere 2 horas de moldeado, 3 de pintura y una de montaje. La fabricación del modelo Víz requiere tres horas de moldeado, 2 de pintura y una de montaje. Las secciones de moldeado y pintura disponen, cada una, de un máximo de 1.500 horas cada mes, y la de montaje de 600.Si el modelo Bae se vende a 10.000 pesetas y el modelo Viz a 12.000 pesetas, ¿qué cantidad de sombreros de cada tipo ha de fabricar para maximizar el beneficio mensual?
7) Cada mes una empresa puede gastar. Como máximo, 1 .000.000 Ptas. en salarios y 1.800.000 Ptas. en energía (electricidad y gasoil). La empresa sólo elabora dos tipos de productos A y B. Por cada unidad de A que elabora gana 80 Ptas. y 50 Ptas. por cada unidad de B. El coste salarial, y energético que acarrea la elaboración de una unidad del producto A y una del B aparece en la siguiente tabla:
|
|
A |
B |
|
Coste salarial |
200 |
100 |
|
Coste energético |
100 |
300 |
Se desea determinar cuántas unidades de cada uno de los productos A y B debe producir la empresa para que el beneficio sea máximo, (Universidades Andaluzas. Septiembre 1997)
8) Una persona tiene 500.000 pesetas para invertir en dos tipos de acciones A y B. El tipo A tiene bastante riesgo con un interés anual del 10% y el tipo B es bastante seguro con un interés anual del 7%. Decide invertir como máximo 300.000 pesetas en A y como mínimo 100.000 pesetas en B, e invertir en A por lo menos tanto como en B. ¿Cómo deberá invertir sus 500.000 pesetas para maximizar sus intereses anuales?
9) Una industria vinícola produce vino y vinagre. El doble de la producción de vino es siempre menor o igual que la producción de vinagre más cuatro unidades. Por otra parte, el triple de la producción de vinagre sumado con cuatro veces la producción de vino se mantiene siempre menor o igual a 18 unidades. Halla el número de unidades de cada producto que se deben producir para alcanzar un beneficio máximo, sabiendo que cada unidad de vino deja un beneficio de 800 Ptas. y cada unidad de vinagre de 200 Ptas.
10) Un hipermercado necesita como mínimo 16 cajas de langostino, 5 cajas de nécoras y 20 de percebes. Dos mayoristas, A y B, se ofrecen al hipermercado para satisfacer sus necesidades, pero sólo venden dicho marisco en contenedores completos. El mayorista A envía en cada contenedor 8 cajas de langostinos, 1 de nécoras y 2 de percebes. Por su parte, B envía en cada contenedor 2, 1 y 7 cajas respectivamente. Cada contenedor que suministra A cuesta 210.000 Ptas., mientras que los del mayorista B cuestan 300.000 pesetas cada uno. ¿Cuántos contenedores debe pedir el hipermercado a cada mayorista para satisfacer sus necesidades mínimas con el menor coste posible?
11) Imaginemos que las necesidades semanales mínimas de una persona en proteínas, hidratos de carbono y grasas son 8, 12, 9 unidades respectivamente. Supongamos que debemos obtener un preparado con esa composición mínima mezclando los productos A y B cuyos contenidos por kilogramo son los que se indican en la siguiente tabla:
Proteínas Hidratos Grasas Coste(kg)
Producto A 2 6 1 600
Producto B 1 1 3 400
¿Cuántos kilogramos de cada producto deberán comprarse semanalmente para que el costo de preparar la dieta sea mínimo?
12) Podemos comprar paquetes de abono A o B. Cada paquete contiene las unidades de potasio (K), fósforo (P) y nitrógeno (N) indicadas en la tabla, donde se da el precio del paquete.
Marca K P N Precio
A 4 6 1 15
B 1 10 6 24
¿En qué proporción hay que mezclar ambos tipos de abono para obtener al mínimo precio un abono que contenga 4 unidades de K, 23 de P y 6 de N?
