Octubre 2008
Dados los siguientes entornos
I)
![]() II)
II)
![]()
Escríbelos por medio de intervalos.
Respreséntalos en la recta real.
Realiza las siguientes operaciones:
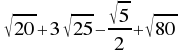
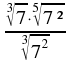
![]()
Racionaliza:
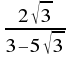
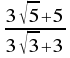
![]()
Halla el valor de x a partir de la definición de logaritmo:
![]()
![]()
![]()
![]()
Sabiendo que
![]() calcula:
calcula:
a) ![]() b)
b)
![]() c)
c)
![]() d)
d) ![]()
¿Cuántos años se necesitan para que 100 € al 20 % anual se conviertan en un millón de euros.?
Noviembre 2008
Halla el valor de m para que el
polinomio:![]() al dividirlo por x+2 el resto sea 1.
al dividirlo por x+2 el resto sea 1.
Factoriza el polinomio
![]()
Resuelve:
![]()
Sin calculadora y sabiendo que
![]() y
y
![]() halla
halla
![]()
![]()
![]()
Resuelve el sistema:
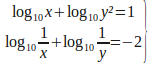
Resuelve el sistema:
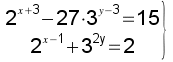
El número de miembros de una población se duplica cada 15 años. Si al principio hay 50 individuos. ¿Cuántos años habrán de pasar para que la población cuente con más de 5000 miembros.?
Diciembre 2008
Halla el valor de x
![]()
![]()
![]()
![]()
Resuelve las siguientes ecuaciones:
![]()
![]()
Resuelve el sistema
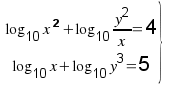
Halla el valor s para que del
polinomio
![]() sea
divisible por
sea
divisible por
![]()
Descompón factorialmente el
polinomio
![]()
Resuelve la ecuación
![]()

Enero 2009
Halla el valor
de a para que al dividir el polinomio :![]() por
(x -2) el resto sea 12.
por
(x -2) el resto sea 12.
Resuelve las siguientes inecuaciones:
![]()
![]()
Resuelve el sistema:
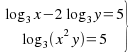
Resuelve:
![]()
Resuelve:
![]()
Soluciones :
Aplicando el
teorema del resto
![]()
![]()
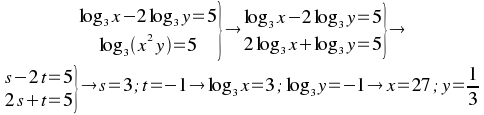
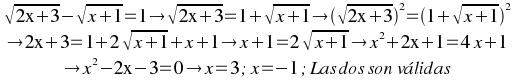
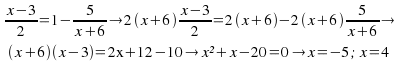
Febrero Trigonometría
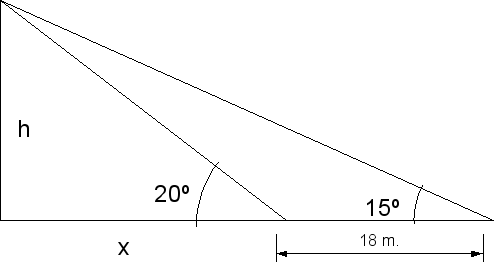
La altura de una torre se ve desde
un ángulo de 15º y al aproximarnos 18m. desde un ángulo de 20º
¿Cuál es la altura de la torre.
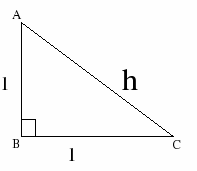
Demuestra las razones
trigonométricas de un ángulo de 45º.
Halla los valores de α
correspondientes a la primera circunferencia que cumplen:
![]()
![]()
![]()
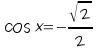
Expresa en radianes los siguientes ángulos:
150º
270º
-30º
240º
Simplifica las siguientes
expresiones:
![]()
![]()
![]()
Soluciones:
1)

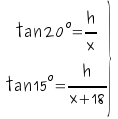
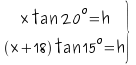
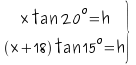
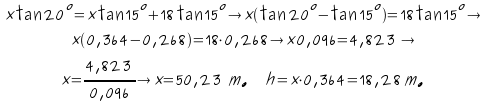
2)
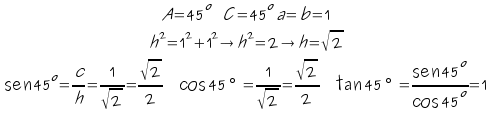
3)
a ) El coseno es positivo en el primer y cuarto cuadrante.
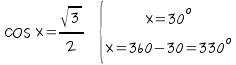
b) El seno es positivo en el 1º y 2º cuadrante.
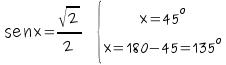
c)
La tangente es positiva en el 1º y 3º
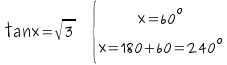
d) El coseno es negativo en el 2º y 3º
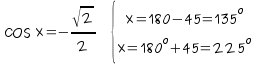
4)
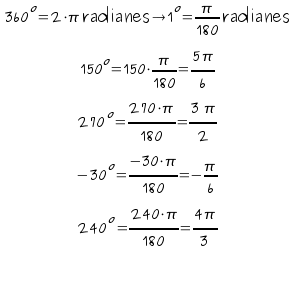
5)
![]()
![]()
![]()
Geometría
4º ESO 2 Abril 2009
Halla las ecuaciones vectorial,
paramétricas, continua, implícita y explícita de la recta que
pasa por los puntos A (1 , 3) B (-3 , 5).
Dados los puntos P (3 , 5) Q (5
, 3) Halla la ecuación de la recta perpendicular al segmento PQ y
que pasa por su punto medio.
Dadas las rectas :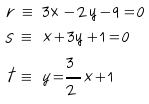
Halla la recta paralela a t que pasa por el punto de
intersección de r y s
Calcula el ángulo que forman las
dos rectas siguientes: 3x +2y -3 = 0 , y = 3x -1
Halla la distancia entre los puntos de corte de la recta 3x -2y + 6 = 0 con los ejes de coordenadas.
4 -05-2009 Funciones
Halla dominio de definición. Puntos de corte con los ejes y signo de las funciones:
a)
![]()
b)
![]()
![]()
Halla dominio de definición y puntos de corte con los ejes:
a) ![]()
b) ![]()
![]()
Calcula la función inversa y comprueba el resultado
![]()
Álgebra 7 Mayo 2009
-
Racionaliza.![]()
Calcula:![]()
Halla el valor de m para que al dividir el polinomio
![]() por
x+3 el resto sea 1.
por
x+3 el resto sea 1.
Factoriza el polinomio
![]()
Resuelve:![]()
Resuelve![]()
Soluciones:
1-a
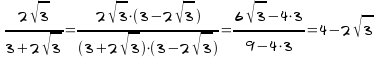
1-b
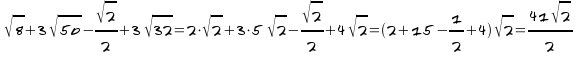
2)
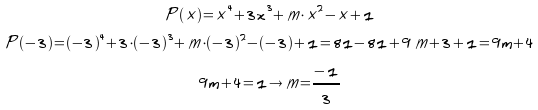
 3)
3)
1 -4 -3 +18
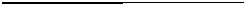 -2 -2 +12 -18
-2 -2 +12 -18
1 -6 +9 0
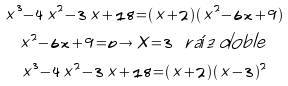
4)
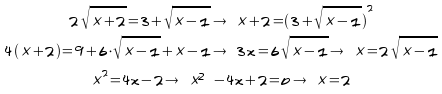
5)
![]()

solución
![]()
Logaritmos Mayo 2009
Pasa a forma
algebraica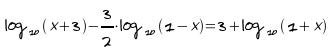
Sabiendo
que:![]()
Calcula:![]()
Resuelve la
ecuación:![]()
Resuelve :
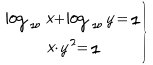
Trigonometría Mayo 2009
Sabiendo que
![]() y
que el ángulo está en el tercer cuadrante calcula el resto de las
razones trigonométricas.
y
que el ángulo está en el tercer cuadrante calcula el resto de las
razones trigonométricas.
Demuestra el valor de las razones
trigonométricas de 30º y 60º
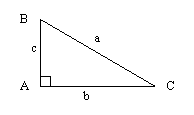
Calcula
los ángulos y lados que faltan en los siguientes triángulos:
a= 9 cm c = 2 cm.
b=3 cm. c = 5cm.
B = 25º
El punto más alto de un árbol
centenario lo vemos bajo un ángulo de 22º al acercarnos 25 m. el
ángulo es de 32º . Halla la altura del árbol.
Simplifica las siguientes
expresiones:
![]()
![]()
![]()
Geometría Mayo 2009
Halla las ecuaciones vectorial, implícita y explicita de la recta
que pasa por los puntos
A(-1 , 3) B( 2 , 1)
¿Cuál es la
pendiente de la recta?
-
Ecuación de la recta paralela a la calculada en el ejercicio anterior y que pasa por el punto (0 , 4)
Ecuación de la perpendicular a la misa recta y que pasa por el
origen de coordenadas.
Dado el triángulo de vértices A(-1 , -3) B(5 , -3) C(3 , 3) Calcula:
Mediatrices de los lados AB y CD
Circuncentro: Punto de corte de las mediatrices.
Dadas las rectas r ≡
x+ 4y = -5 y la recta s ≡
y = -2x +4 Halla el punto de corte y el ángulo que forman
4º ESO Matemáticas B
Trigonometría
1)Halla el valor de todos los ángulos menores de 360º que cumplen:3) Dibuja
un triángulo equilátero de lado 1 , halla el valor de la altura y
demuestra las razones trigonométricas de los ángulos 30º y 60º
1.a= 9 m , b= 6m.
2.a=4m. B=50º
3.c= 3m. B=20º
6) Halla el valor en radianes:
a) 150º b) 330º c) 270º d) 180º
|
|