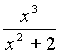FUNCIONES
Problema 1.1: Dada la función f(x) = x4 - x2 , se pide:
-
Determinar los intervalos de crecimiento y decrecimiento, así como los máximos y los mínimos.
-
Determinar los intervalos de concavidad y convexidad
-
Dibujar la gráfica de la función.
Problema 1.2:
Represente gráficamente la función y estudie detalladamente su continuidad y derivabilidad:
Represente gráficamente la función f(x) = sen (| x| ) y
estudiese su continuidad y derivabilidad.
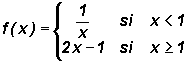 ,
,
estudia su continuidad y dibuje su gráfica.
Problema 1.5: Estudie los intervalos de crecimiento y decrecimiento y los extremos relativos de la función f(x) = |x 2 - 1|.
-
Halla la ecuación de la recta tangente a la parábola y = x2 -3x+5 en el punto de abscisa x = 3. Calcula el ángulo que forma dicha recta tangente con la dirección positiva del eje de abcisas.
-
¿En qué punto de la gráfica de la parábola la recta tangente forma un ángulo de 33º con la dirección positiva del eje de abcisas. (Si conoces el ángulo conoces la pendiente "m" de la recta tangente, y la pendiente de la recta tangente debe coincidir con el valor de la derivada en el punto buscado)
-
Si la recta tangente es horizontal en cierto punto, ¿ese punto es generalmente algún punto especial de la gráfica de la parábola?
-
Encuentra las coordenadas del punto mencionado en el apartado c,
Dibuja la gráfica de la parábola
6) Consideramos la función f(x) = 2/x. ¿Cuál es su gráfica? Halla la ecuación de la recta tangente en el punto de abcisa 5. Halla el área del triángulo que determina esa recta tangente con los ejes de coordenadas
7) Halla el valor de "c" para que la función f(x) = x2 – cx + 12 alcance en x = 7/2 un mínimo. Dibuja la gráfica
8)
Estudia el crecimiento de las funciones y = x, y = x3, y =
x2,
y = x2 –1.
9) De la función y = x2 –ax + b se sabe que alcanza un mínimo en el punto de abcisa 2, y que la gráfica de la función pasa por el punto P(4, 4). Calcula "a" y "b" y halla la ecuación de la recta tangente a la gráfica en P.
10) Estudia la curvatura de las funciones f(x) = x2, g(x) = x3, h(x) = 1/x. Dibuja las tres gráficas
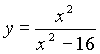
11) Estudia el crecimiento, la concavidad y convexidad de las funciones:
y = ln(x)
, y =
ex+1, y = ![]()
12) Halla el dominio y los puntos de intersección de la gráfica de con los ejes de coordenadas. Estudia su crecimiento y su curvatura.
Halla la ecuación de la recta tangente a la gráfica de f(x) = x3 –2x2 + 3x – 1 en su punto de inflexión.
Estudia el crecimiento de:
![]()