Dibujamos en el plano dos rectas fijas perpendiculares entre sí que llamaremos eje X o eje de abscisas y eje Y o eje de ordenadas. Al punto de corte O le llamaremos origen de coordenadas. En cada eje elegimos un segmento de longitud unidad y el sentido positivo.
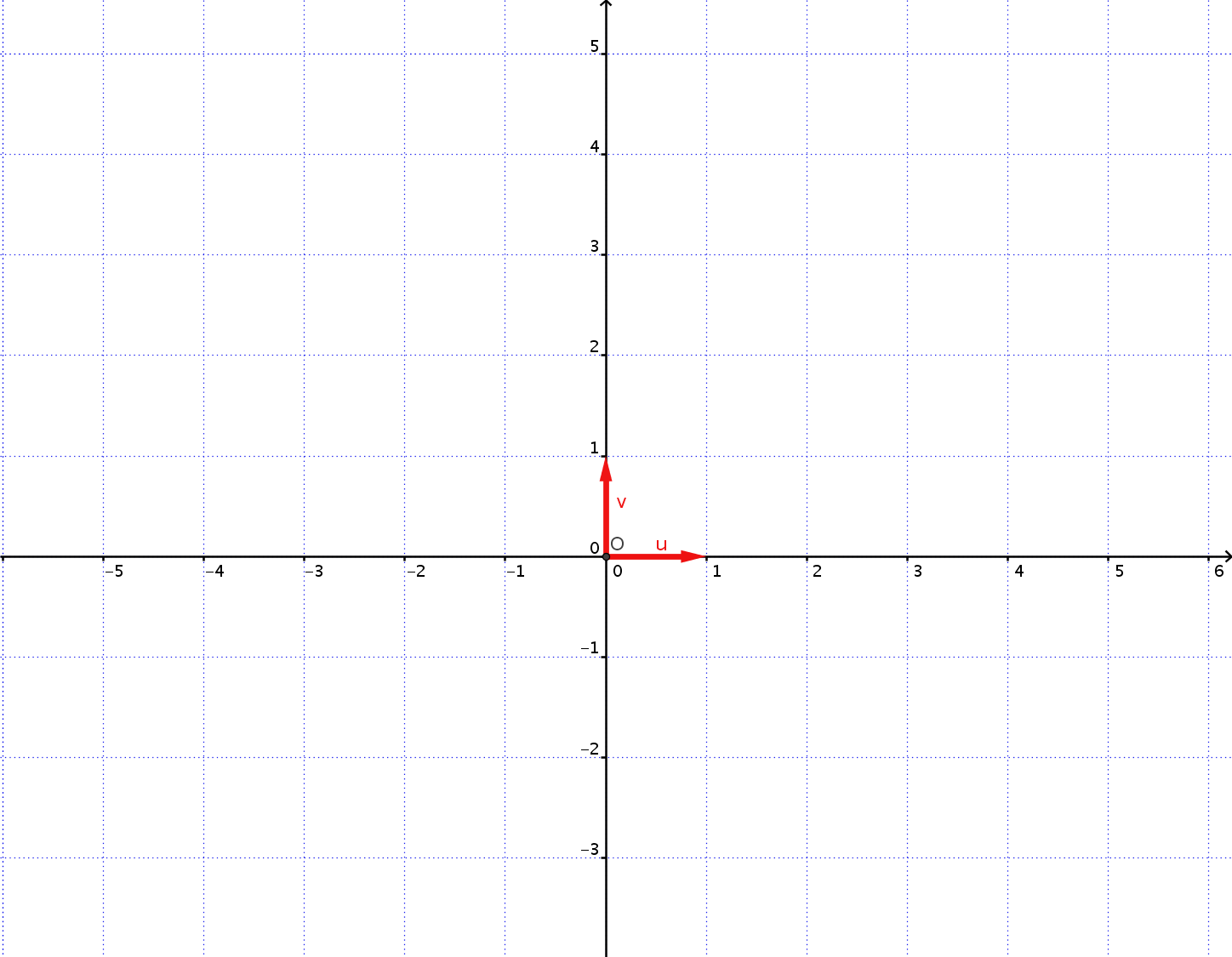
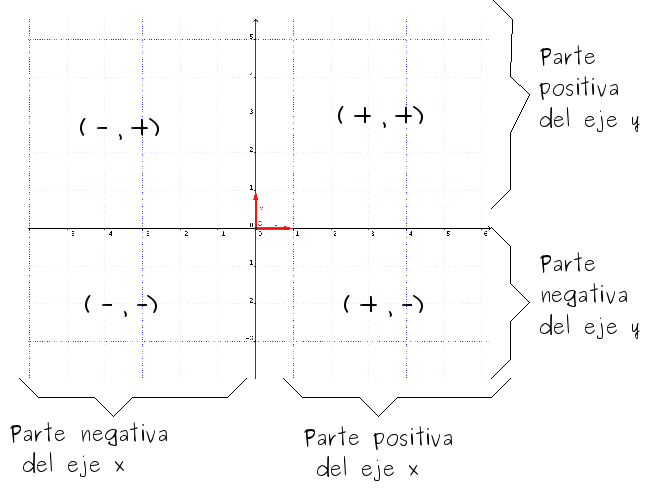
Una vez definidos los ejes, a cada punto del plano le podemos asociar don números, sus distancias al eje de las Y (abscisa o coordenada x) y distancia al eje X (ordenada o coordenada y). Dependiendo del cuadrante los signos serán positivos o negativos.
Recíprocamente, a cada par de números en un determinado orden (x , y) le corresponde un punto del plano y solo uno que tiene dicha abscisa y ordenada.
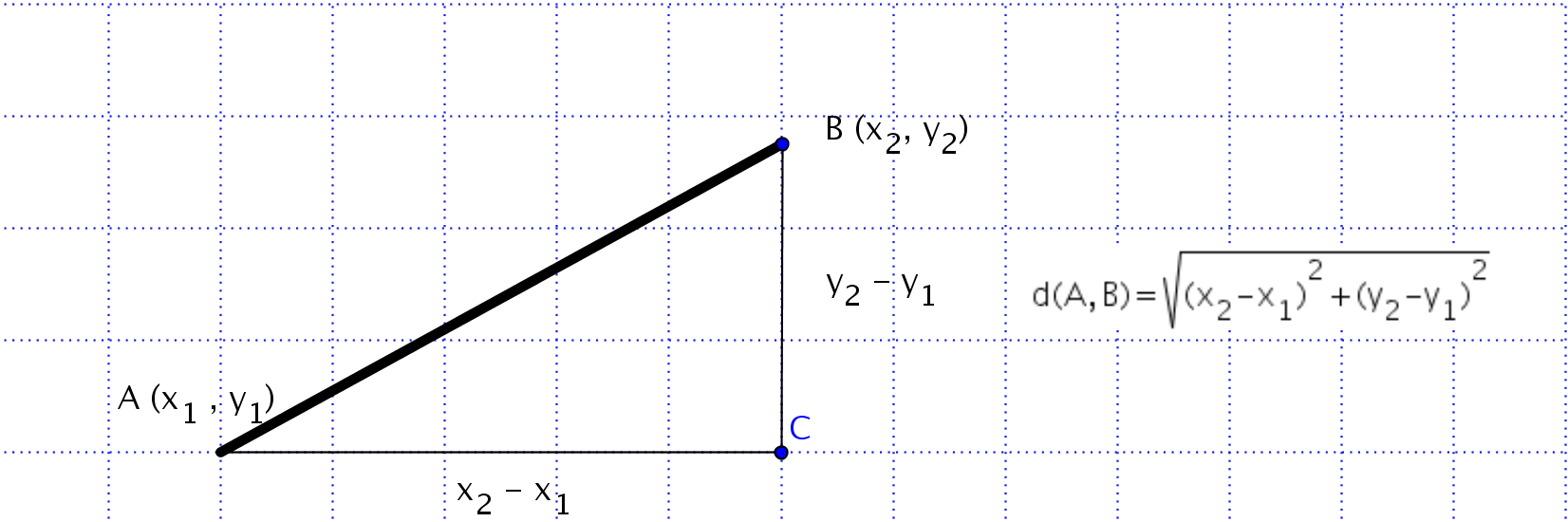
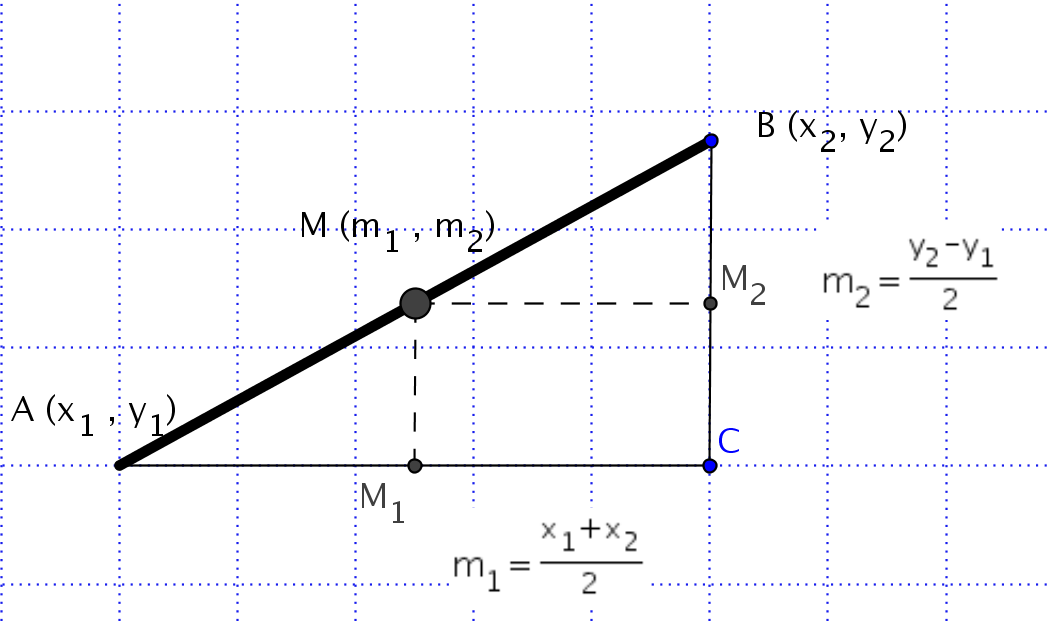
Las coordenadas del punto medio de un segmento son la suma de las coordenadas dividido por dos.
Un vector fijo es un segmento orientado que tiene su origen en un punto fijo y su extremo en otro.
Un vector fijo queda determinado:
Por la longitud del segmento que llamaremos módulo del vector.
Dirección de la recta que lo contiene.
Sentido: Uno de los dos que tiene la recta.
Origen del segmento.
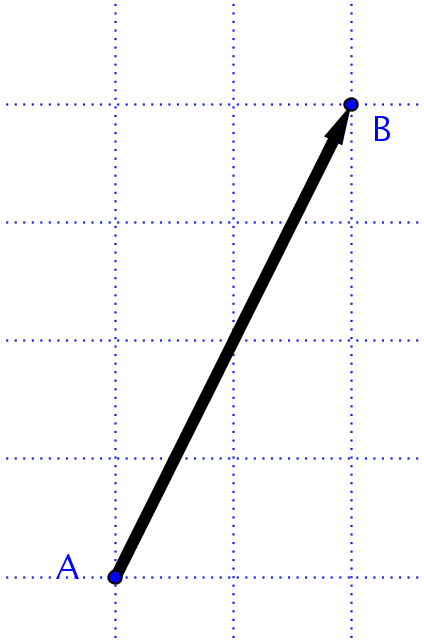
Un vector libre es un segmento orientado con independencia de donde este situado. Está determinado por su módulo, dirección y sentido . En la imagen de abajo hay 5 vectores fijos y solamente dos libres:
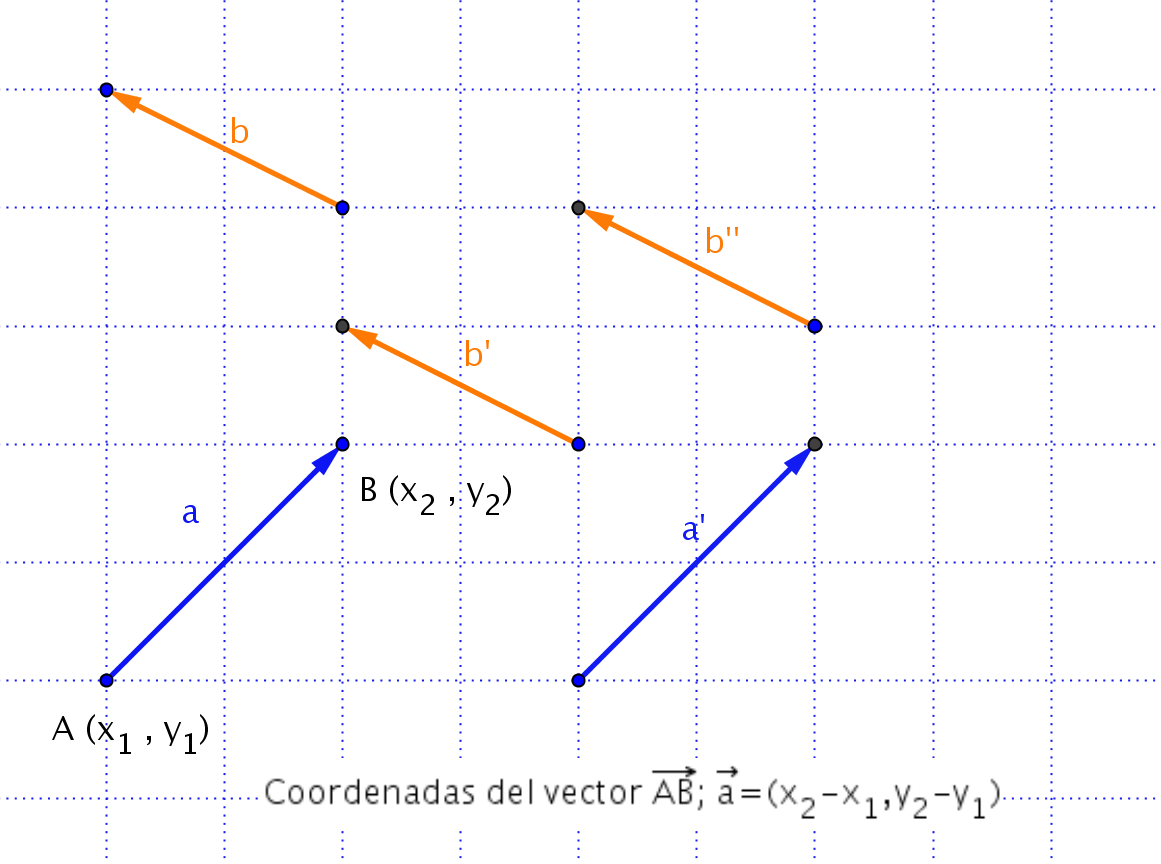
Las componentes o coordenadas cartesianas de un vector son las coordenadas del extremo del vector menos las coordenadas del origen. A partir de ahora siempre que hablemos de vectores nos referimos a vectores libres.
Para multiplicar un vector pro un número k se multiplica el módulo del vector por el número real, la dirección se queda igual y el sentido no varia si el número es positivo y cambia si es negativo.
Para sumar vectores se representan un a continuación del otro y el vector suma será el que une el origen del primero con el extremo del último.
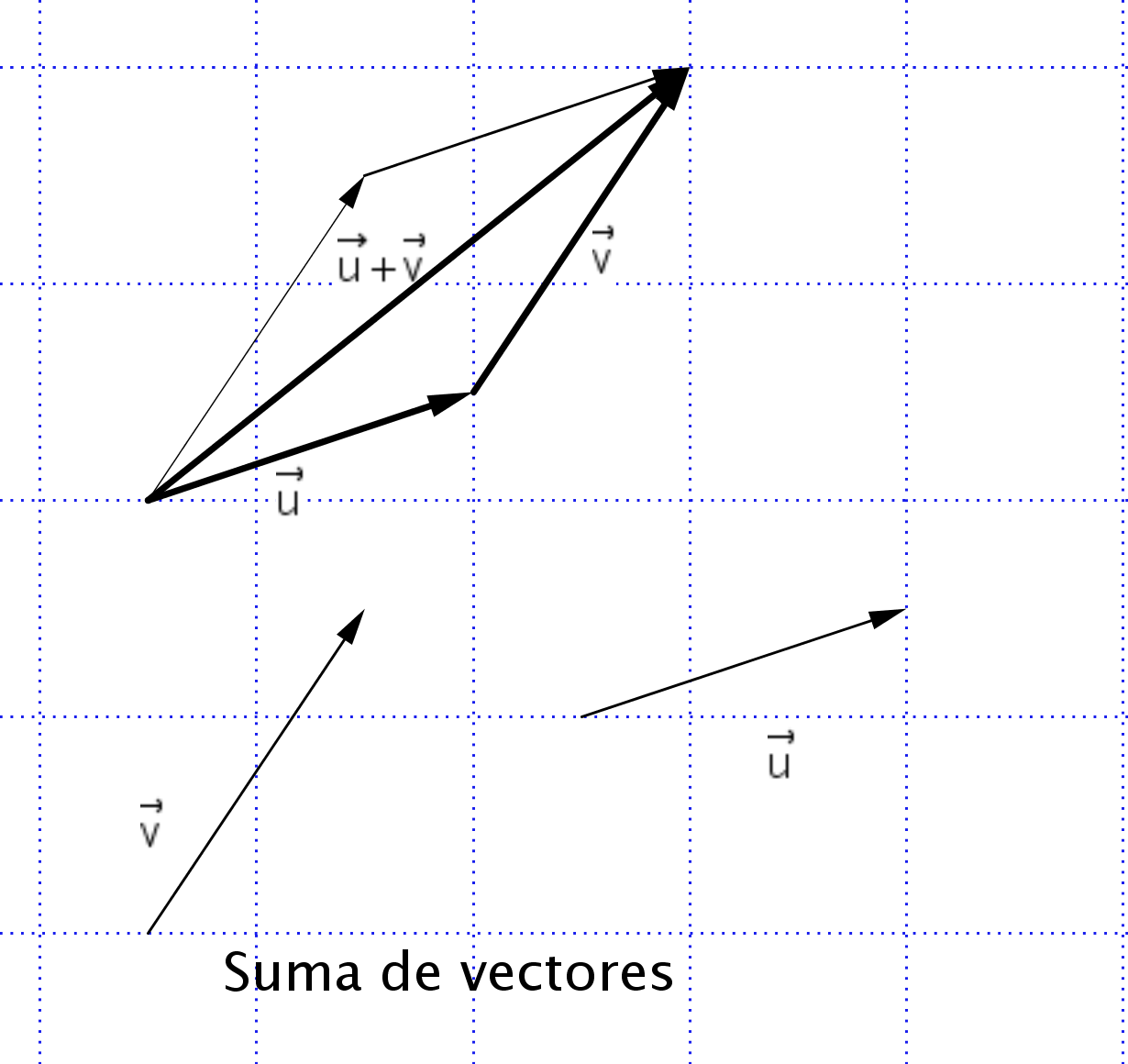
Un vector u es combinación lineal de los vectores v y w si lo podemos poner de la forma u = a ·v + b ·w siendo a y b números reales.
Consideremos los vectores de módulo la
unidad y dirección la de dos ejes de coordenadas: i = (1,0)
, j = (0
, 1).
Cualquier vector z de componentes z = (x1 , y1) lo podemos poner como z = x1 i + y1 j
Las coordenadas del vector suma de otros dos son la suma de las coordenadas de los dos vectores
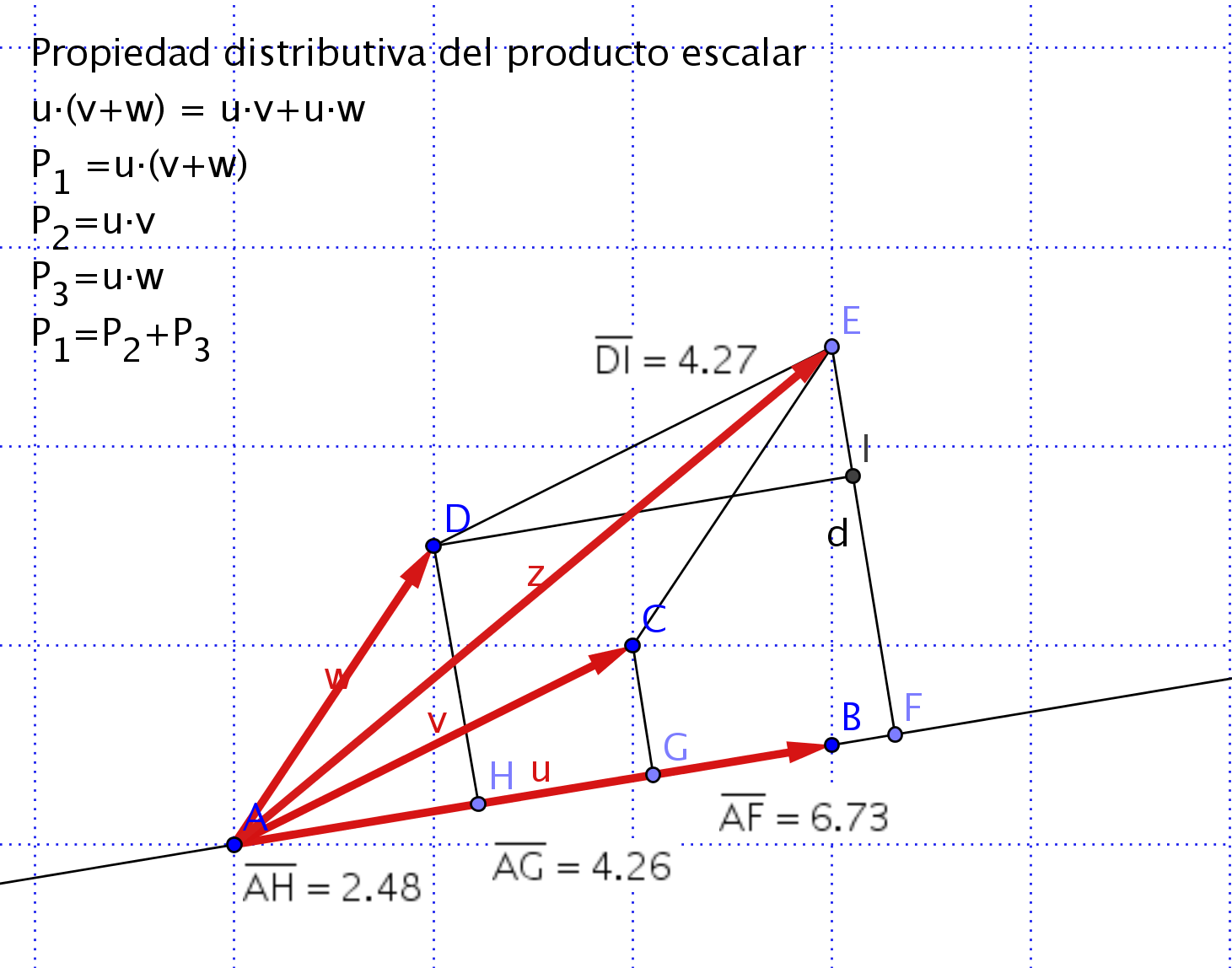
1)
1 Calcula el punto medio de los segmentos de extremos A y B:
a) A(1 , -2) B(3 , 3)
b) A(2 , 1) B (1 , 2)
2)
Calcula el punto medio de los segmentos de extremos A y B:
3)
De los siguientes vectores agrupa los que tengan la misma dirección.
5)
Dado los puntos A( -2 , 7) B(3 , -5) halla las coordenadas del punto medio del segmento AB.
6)
Dado el punto A(-1 , 3) halla las coordenadas del punto B para que M(1 , 5) sea el punto medio del segmento AB. Calcula la longitud del segmento BM
7)
Halla λ para que los siguientes vectores sean paralelos:
8)
Halla λ para que los vectores anteriores sean perpendiculares.
9)
Calcula:
10)
Dado los puntos A(-1 , 2 ) B(3 , 5), hallad un punto P tal que:
11
Dado el triángulo formado por los puntos A(0 , 5) B(-2 , -2) C(3 , 0) Hallad la longitud de sus lados y el valor de sus ángulos.
Ecuación vectorial de una recta:
Recta definida por un punto y un vector:
Ecuación vectorial:
Ecuaciones paramétricas:
Igualando la componentes de los vectores:
Ecuación continua
Ecuación general o implícita.
Si en la igualdad anterior quitamos denominadores y pasamos todo a un miembro queda:
La ecuación anterior se puede poner como:
Ecuación punto pendiente:
Ecuación explícita:
donde m es la pendiente de la recta y h la ordenada en el origen.
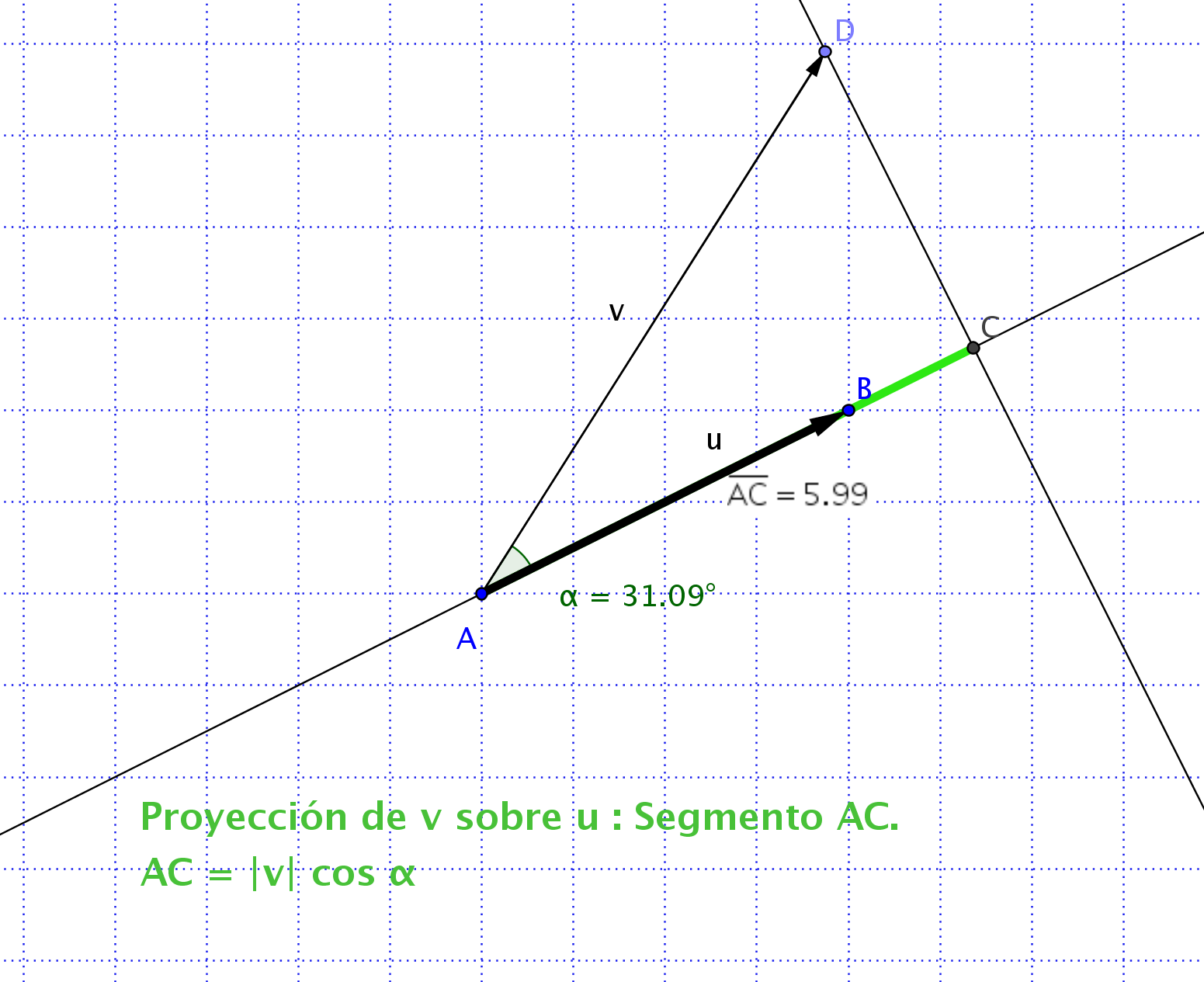
Distancia de un punto a una recta
Halla la ecuación de la recta en forma vectorial, paramétrica, implícita y explícita en los siguientes casos:
2)
Dado un punto y un vector, halla la ecuación vectorial, continua y ecuaciones paramétricas para los siguientes casos:
Halla la ecuación explicita para las rectas que pasan por los siguientes puntos:
Dada la recta r ≡ 3x-2y+8=0 Calcula:
5)
Dada las rectas
Calcula:
6)
Dado el triángulo formado por los puntos: A(2 , 3) B(-4 , 2) C(2 , 0) calcula:
Dado el triángulo formado por los puntos: A(1 , 1) B(5 , 3) C(7 , -2) calcula las coordenadas del baricentro y del incentro.
8)
Halla el valor de k para que las rectas de ecuaciones :
1)
Halla el centro y el radio de las siguientes circunferencias
Halla la ecuación de la circunferencia determinada por tres puntos:
a) A(-1 , 0) B(1, 1) C(0, 4)
3)
Halla la posición relativa de la recta 2x-y-3=0 respecto de la circunferencia.
x²+y² -3x+3y+2=0
4)
Calcula la ecuación de la circunferencia que pasa por los puntos P(6 , 3) Q(-2 , -5) y tiene el centro en la recta x-3y-17=0
5)
Hallad los elementos característicos de las elipses:
Hallad la ecuación de una elipse para los siguientes casos:
Halla la ecuación de la hipérbola:
10)
Para las siguientes parábolas calcular sus elementos: