|
Hay magnitudes que no siempre tiene el mismo valor: el tiempo que se tarda en hacer un determinad trayecto no es siempre el mismo; la cotización en bolsa de un determinado paquete de acciones; los litros de agua por metro cúbico caídos en un determinado año; velocidad de un cuerpo en caída libre.
Hay otras magnitudes que son constantes: la temperatura de ebullición del agua en condiciones normales; equivalencia en pesetas de un euro; aceleración de la gravedad; valor de pi.
Muchas veces las variables están relacionadas unas con otras, de modo que a cada valor de una dada, le corresponde un determinado valor de otra. La noción de función establece una relación entre dos o más variables. Es uno de los conceptos más importantes en matemáticas y aparece por primera vez de forma explícita a finales del siglo XVII y principios del XVIII. Leibniz y los Bernoulli lo utilizaron ampliamente y Euler utilizó el símbolo f(x).
Para una expresión como
Definiciones:
Regla que asocia a cada número real, otro número real
Correspondencia que asocia a cada elemento de un conjunto de números otro número.
Todos los valores de la variable independiente para los cuales podemos encontrar un valor de la función.
Notación:
Una función puede venir dada por una tabla de valores, una gráfica, o una expresión analítica (fórmula) y está puede ser explícita o implícita.
Ejercicios:
Calculad el dominio de definición de las siguientes funciones:
1)
2)
3)
4)
5)
Soluciones
1)
El dominio de definición es el conjunto de valores de x para los cuales se puede calcular la función como son raíces cuadradas, serán todos los valores de x que hagan positivo lo que está dentro de la raíz:
2) Se pueden calcular siempre que no sea cero el denominador, por tanto el dominio de definición serán todos los reales excepto los que anulen al denominador.
3) La función exponencial se puede calcular siempre que exista el exponente, por tanto el dominio de definición serán todos lo reales R.
5) Siempre que se pueda calcular las dos raíces

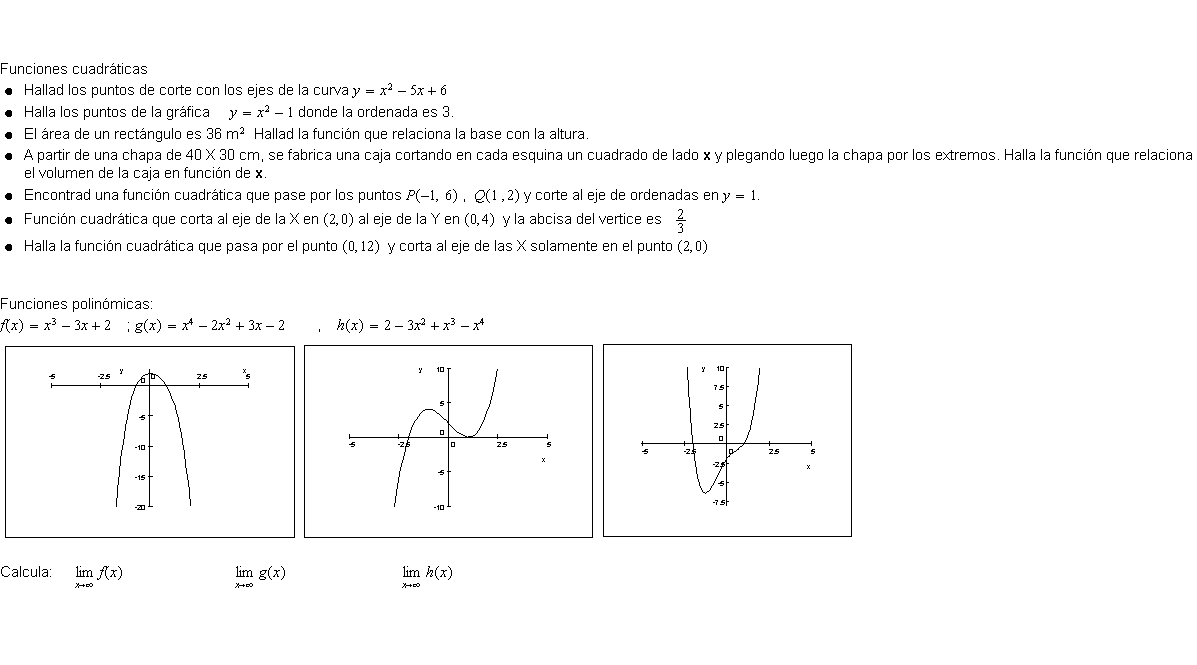
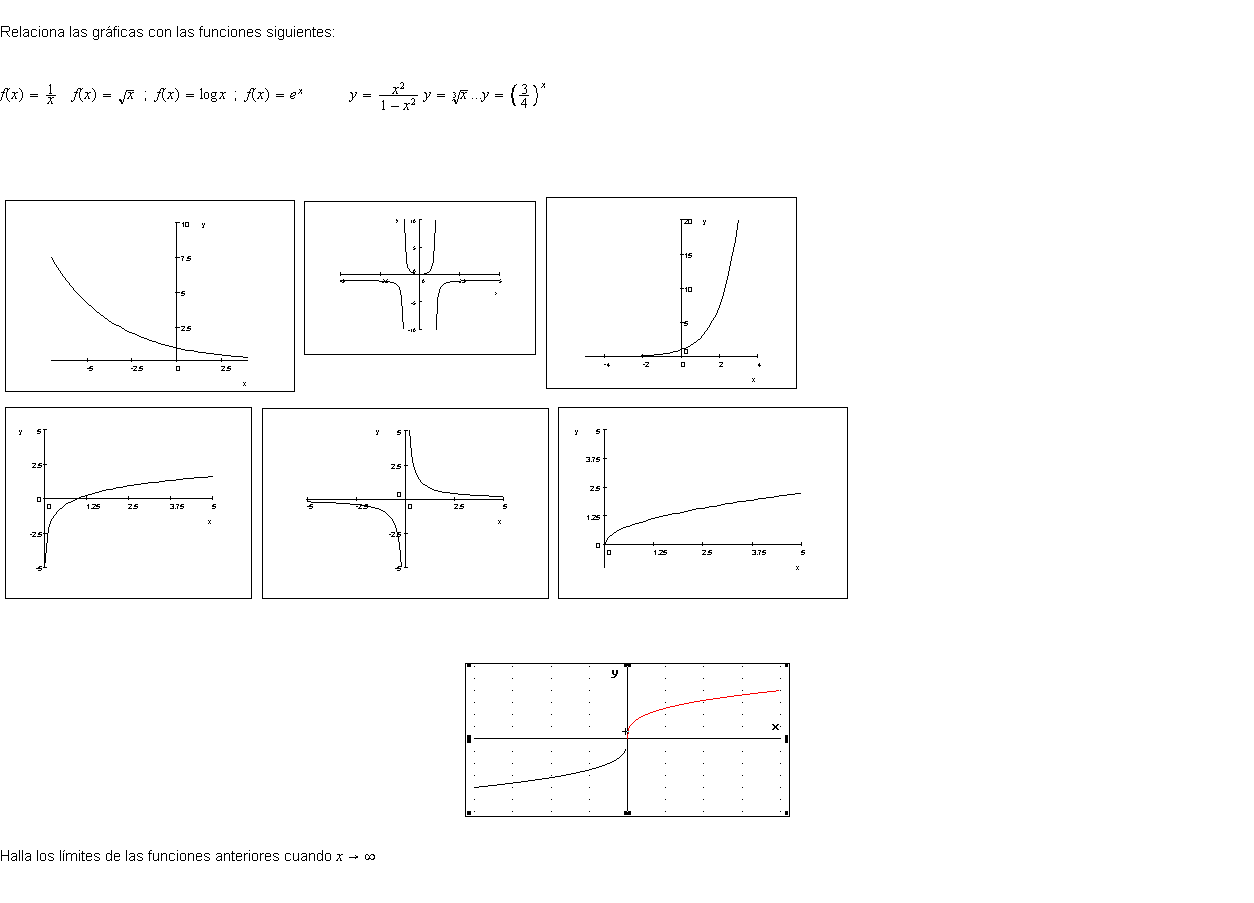
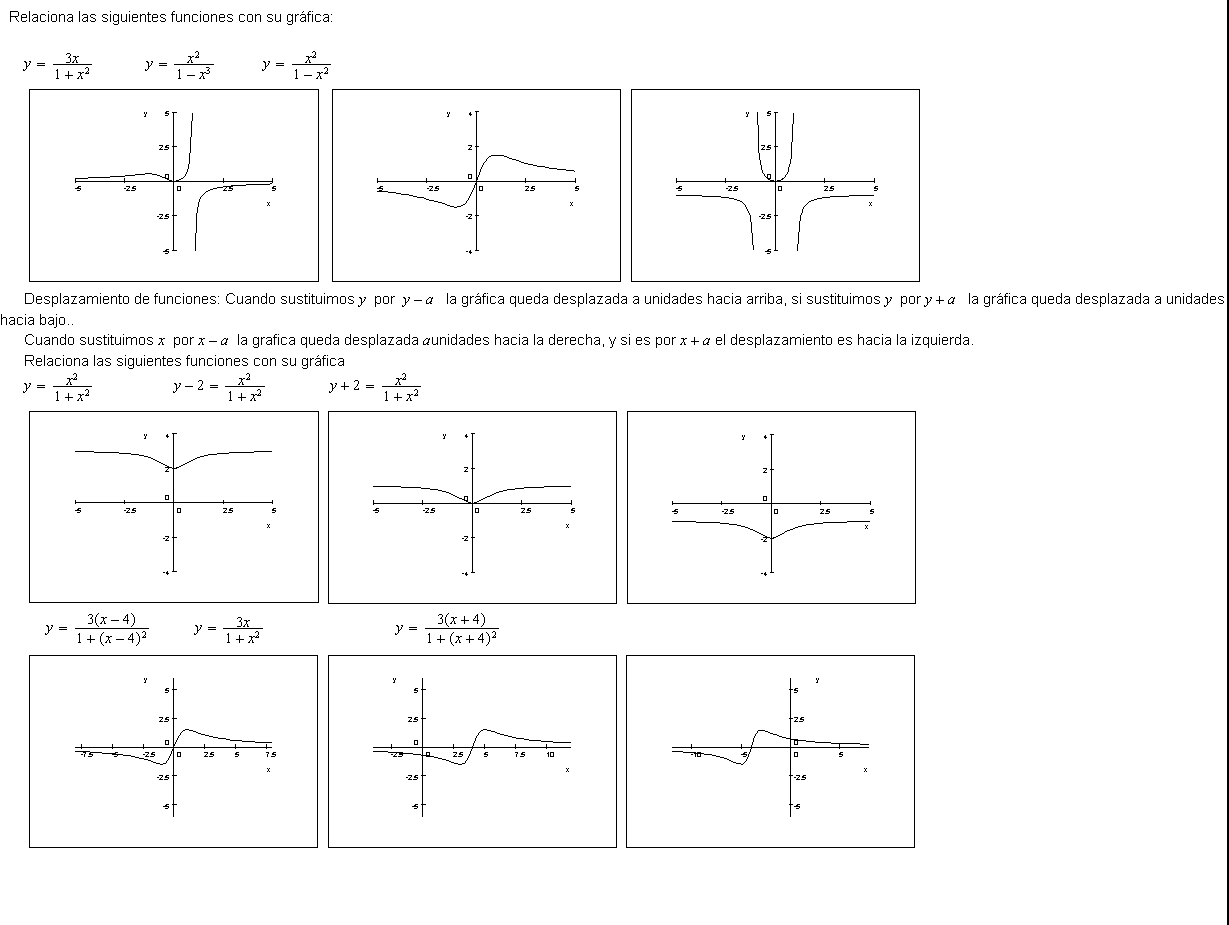
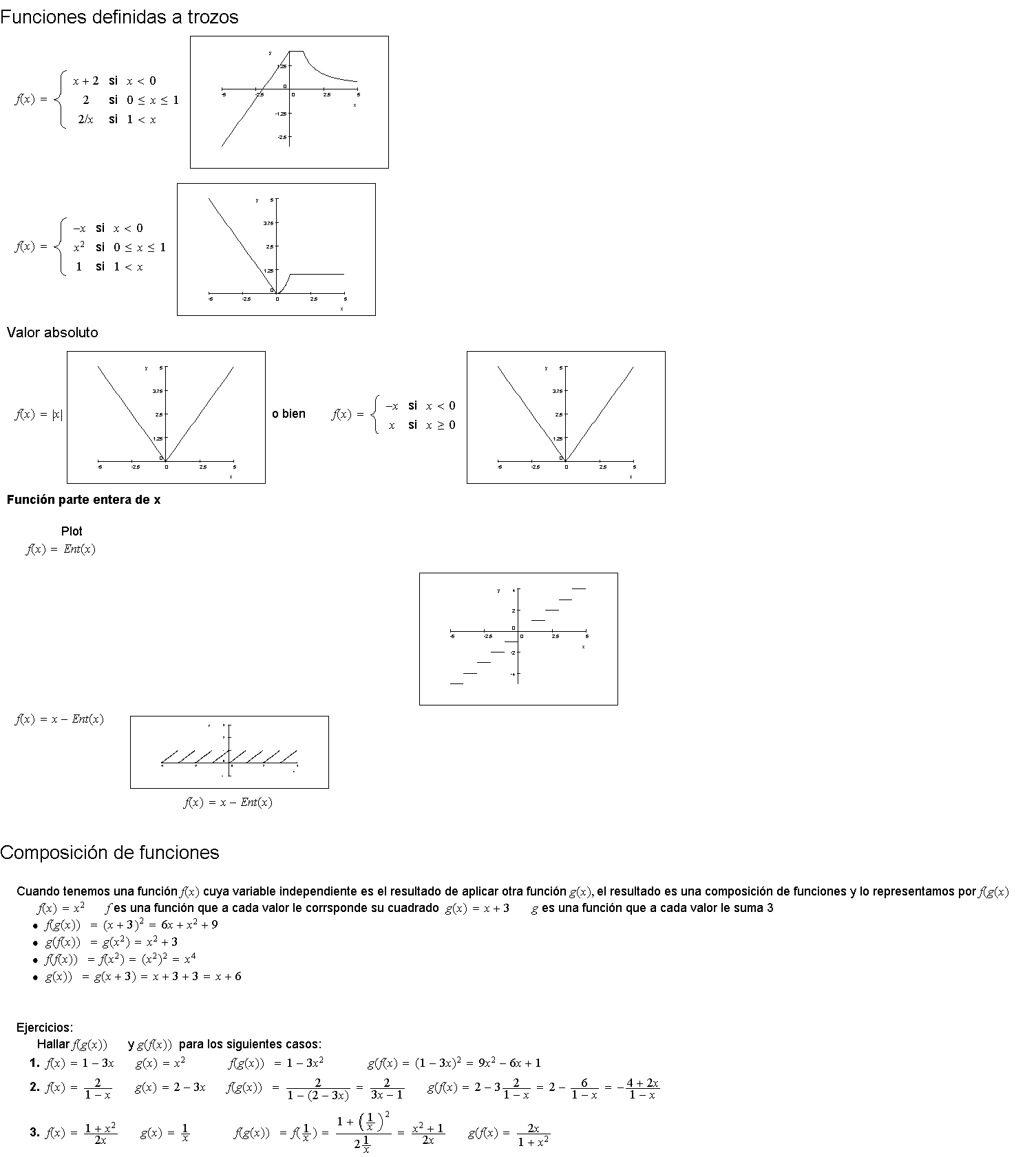
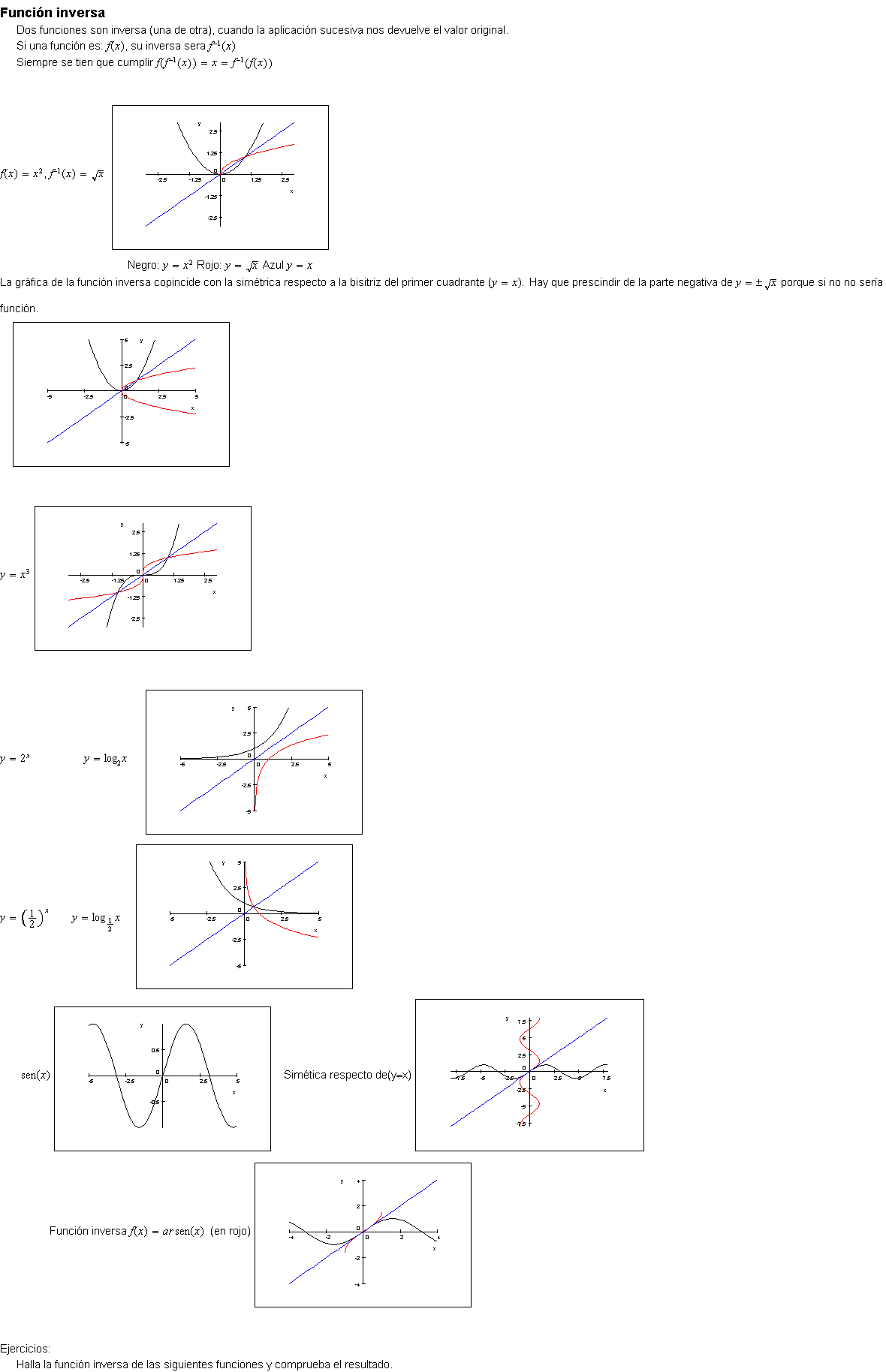

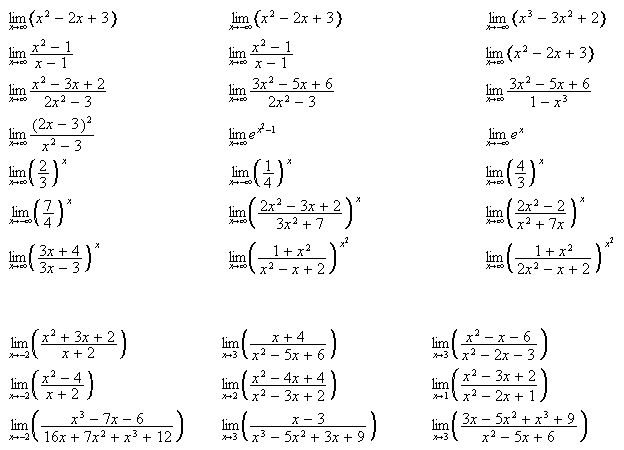
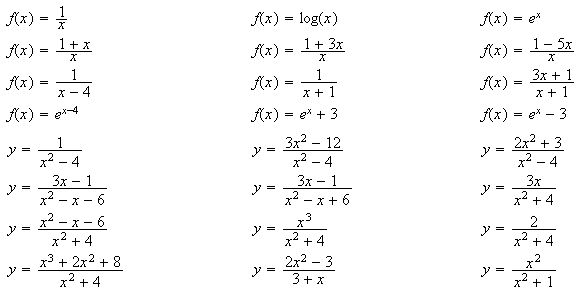
Para las funciones anteriores halla:
Dominio de definición
Continuidad
Simetrías
Signo de la función
Comportamiento de la gráfica respecto de las asíntotas verticales.